–ассмотрим результат наблюдений ’ за посто€нной физической величиной Q как случайную величину, принимающую различные значени€ Z, в различных наблюдени€х за ней. «начени€ Xi будем называть результатами отдельных наблюдений.
»з теории веро€тности следует, что наиболее универсальный способ описани€ случайных величин заключаетс€ в отыскании их интегральных или дифференциальных функций распределени€.
ѕод интегральной функцией распределени€ результатов наблюдений понимаетс€ зависимость веро€тности того, что результат наблюдени€ Xi в i -м опыте окажетс€ меньшим некоторого текущего значени€ х, от самой величины х:
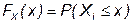 .
.
«десь и в дальнейшем большие буквы используютс€ дл€ обозначени€ случайных величин, а маленькие Ц значений, принимаемых случайными величинами. ѕоскольку функци€ распределени€ веро€тности представл€ет собой веро€тность, то она удовлетвор€ет следующим свойствам:
Ц  при
при 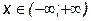 ,
,
Ц  ,
,  , т.е. расположена в диапазоне от 0 до 1,
, т.е. расположена в диапазоне от 0 до 1,
Ц  Ц неубывающа€ функци€ x, т.е.
Ц неубывающа€ функци€ x, т.е.  , если
, если 
Ц  Ц веро€тность нахождени€ случайной величины x в диапазоне от x1 до x2.
Ц веро€тность нахождени€ случайной величины x в диапазоне от x1 до x2.
Ќа рисунке 3 показан пример функции распределени€ веро€тности.

–ис. 3
Ѕолее нагл€дным €вл€етс€ описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределени€, иначе называемой плотностью распределени€ веро€тностей:
 .
.
‘изический смысл p(x) состоит в том, что произведение f(x)dx представл€ет веро€тность попадани€ случайной величины ’ в интервал от х до х + δx, т.е.
 .
.
—войства плотности распределени€ веро€тности:

Ц веро€тность достоверного событи€ равна 1; иными словами, площадь, заключенна€ между кривой дифференциальной функции распределени€ и осью абсцисс, равна единице.

Ц веро€тность попадани€ случайной величины в интервал от x1 до x2 и равна площади под кривой p(x) между абсциссами x1 и x2 (рис.4).

–ис. 4
ќт дифференциальной функции распределени€ легко перейти к интегральной путем интегрировани€:
 .
.
—уммарна€ погрешность складываетс€ из нескольких составл€ющих с различными плотност€ми распределени€ P1(x),P2(x)ЕPn(x). ѕоэтому возникает задача определени€ закона распределени€ погрешности. ƒл€ суммы непрерывных случайных величин X1 и X2, имеющих распределени€ P1(x1) и P2(x2) этот закон называетс€ композицией и определ€ют интегралом свЄртки (рис.5):
 .
.

–ис. 5
Ўирокое распространение нормального распределени€ погрешностей в практике измерений объ€сн€етс€ центральной предельной теоремой теории веро€тностей, €вл€ющейс€ одной из самых замечательных математических теорем, в разработке которой принимали участие многие крупнейшие математики Ц ћуавр, Ћаплас, √аусс, „ебышев и Ћ€пунов. ÷ентральна€ предельна€ теорема утверждает, что распределение случайных погрешностей будет близко в нормальному вс€кий раз, когда результаты наблюдени€ формируютс€ под вли€нием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.
|
|
|






