—огласно √ќ—“ 8.401-80, дл€ указани€ нормированных значений погрешности чувствительности γs, приведЄнной аддитивной погрешности γ0, приведЄнных погрешностей в начале γн и конце γк диапазона измерений не могут использоватьс€ произвольные числа. ¬ыраженные в процентах, они могут иметь значени€ 6 Ц 4 Ц 2,5 Ц 1,5 Ц 1,0 Ц 0,5 Ц 0,2 Ц 0,1 Ц 0,05 Ц 0,02 Ц 0,01 Ц 0,005 Ц 0,002 Ц 0,001 и т. д.
«начение класса точности прибора маркируетс€ на его шкале. ƒл€ того чтобы различить, кака€ из погрешностей обозначена в точности, используютс€ следующие условные обозначени€.
≈сли класс точности прибора установлен по значению погрешности чувствительности γs, т.е. форма полосы погрешности условно прин€та чисто мультипликативной, обозначаемое на шкале значение класса точности обводитс€ кружком. Ќапример,  обозначает, что γs = 1,5%.
обозначает, что γs = 1,5%.
≈сли же полоса погрешностей прин€та аддитивной и прибор в качестве класса нормируетс€ приведЄнной погрешностью нул€ γ0 (таких приборов большинство), то класс точности указываетс€ без каких-либо подчеркиваний (например, просто 1,5).
Ќаконец, на приборах с резко неравномерной шкалой, например омметрах, класс точности прибора указываетс€ в дол€х от длины шкалы и обозначаетс€ 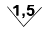 .
.
ќбозначение класса точности в виде, например, 0,02/0,01 указывает, что погрешность прибора нормирована по двучленной формуле с γн = 0,01% и γк = 0,02%.
ќбозначение класса прибора дает достаточно полную информацию дл€ вычислени€ приближЄнной оценки погрешностей результатов измерени€.
Ќекоторые практические замечани€
’от€ √ќ—“ 8.401-80 направлен на то, чтобы нормирование погрешностей —» производилось единообразно, в измерительной практике такого единообрази€ пока ещЄ нет, так как используетс€ большое число хороших высокоточных приборов, которые были выпущены ещЄ до введени€ этого стандарта, закупаютс€ и широко используютс€ приборы иностранного производства, нормированные, естественно, не в соответствии с √ќ—“ 8.401-80, и т. д.
Ќапример, погрешность высокоточных потенциометров посто€нного тока нормируетс€ чаще всего двучленной формулой (*), а класс точности прибора указываетс€ в виде одного числа Ц его относительной погрешности чувствительности. ¬ этом случае указание класса точности в виде одного числа γs не €вл€етс€ признаком того, что прибор не имеет аддитивной составл€ющей погрешности, и потребитель об€зан быть внимательным при расчЄте погрешностей результатов измерени€, чтобы не допустить ошибки.
ѕри нормировании погрешностей сложных —» двучленной формулой (**) √ќ—“ 8.401-80 предусматривает несколько иное ее написание, когда текущее значение относительной погрешности γ(х) выражаетс€ не через значение аддитивной γн и мультипликативной γs составл€ющих предела допускаемых погрешностей, как в формуле (**), а через указываемые в обозначении класса точности приведенные погрешности в начале γн и в конце γк диапазона измерений. ¬ этом случае, учитыва€, что
γк = γн + γs,
|
|
|
соотношение (**) принимает вид
 . (****)
. (****)
Ќа практике это соотношением более удобно использовать дл€ вычислени€ γ(x) по известным х, Xк, γн и γк.
” весьма широкодиапазонных приборов, например, мостов дл€ измерени€ сопротивлений, в их технической документации вместо указани€ коэффициентов трЄхчленной формулы (***) часто привод€тс€ просто диапазоны, в которых погрешность результата измерени€ не превосходит указанного значени€.
Ќапример, указываетс€, что относительна€ погрешность не превосходит:
0,5% в диапазоне от 102 до 104 ќм;
1% Ц от 5 до 105 ќм;
5% Ц от 0,5 до 106 ќм;
10% Ц от 0,2 до 2Ј106 ќм;
20% Ц от 0,1 до 4Ј106 ќм.
Ёти данные достаточно точно соответствуют трЄхчленной формуле (***).
ѕоэтому по ним можно определить коэффициенты Δo, Δ∞ и γs формулы (***) и использовать еЄ дл€ аналитического определени€ γ(х) при любом произвольном значении х.
“ак, например, приведЄнным выше данным соответствует Δo = 0,02 ќм, Δ∞ = 20Ј106 ќм и γs = 0,5%.
ќтсюда дл€ любого х погрешность (в процентах) γ (х) = 100 [0,02/x + 0,5/100 + х/(20Ј106)].






