Класс точности средств измерений

Это характеристика, определяющая гарантированные границы значений основных и дополнительных погрешностей, а также другие свойства средств измерений, влияющих на точность. Соответствие погрешности СИ приписанному им классу точности во время эксплуатации проверяется при периодических поверках. Если погрешность оказывается меньше нормированных значений, то СИ продолжает эксплуатироваться, если нет, то подлежит ремонту и регулировке.

Основные способы установления пределов допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ 8.401-80. Основная погрешность СИ нормируется четырьмя различными способами.

Чтобы четко уяснить себе эти различия и грамотно использовать нормируемые значения при расчете погрешностей результатов измерения, необходимо рассмотреть характер изменения относительной и абсолютной погрешности СИ в диапазоне значений измеряемой величины и обусловленные этим положения стандартов, регламентирующих нормирование погрешностей средств измерений.

Основное различие в способах нормирования обусловлено разным соотношением аддитивной и мультипликативной составляющих в погрешности тех или иных СИ.

При чисто мультипликативной полосе погрешностей абсолютная погрешность Δ(х) возрастает прямо пропорционально текущему значению х измеряемой величины.

Поэтому относительная погрешность, т.е. погрешность чувствительности такого преобразователя

γ _s = Δ (х)/х

оказывается постоянной величиной при любом значении х и её удобно использовать для нормирования погрешностей преобразователя и указания его класса точности.

Таким способом нормируются погрешности масштабных преобразователей (делителей напряжения, шунтов, измерительных трансформаторов тока и напряжения и т.п.). Их класс точности указывается в виде значения γ_s, выраженного в процентах.

Граница относительной погрешности результата измерения γ(х) в этом случае постоянна и при любом х просто равна значению γ_s, а абсолютная погрешность результата измерения рассчитывается по формуле

Δ (х) = γ _s x.

Если бы эти соотношения оставались справедливыми для всего диапазона возможных значений измеряемой величины х от 0 до X_к (X_к – предел диапазона измерений), то такие измерительные преобразователи были бы наиболее совершенными, так как они имели бы бесконечно широкий рабочий диапазон, т.е. обеспечивали бы с той же погрешностью измерение сколь угодно малых значений х.

Однако реально таких преобразователей не существует, так как невозможно создать преобразователь, полностью лишённый аддитивных погрешностей.

Эти погрешности от шума, дрейфа, трения, наводок, вибраций и т. п. неизбежны в любых типах СИ. Поэтому для реальных СИ, погрешность которых нормируется лишь одним числом – погрешностью чувствительности γ_s, – всегда указываются границы рабочего диапазона, в которых такая оценка остаётся приближённо справедливой.

При чисто аддитивнойй полосе погрешностей остаётся неизменной для любых значений х граница абсолютной погрешности нуля

Δ (х) = Δ _o = const.

Но нормировать абсолютное значение Δ_o неудобно, так как для многопредельных приборов оно будет различным для каждого поддиапазона, и в паспорте прибора пришлось бы перечислять эти значения для всех поддиапазонов.

Поэтому нормируют не абсолютное Δ_o, а приведённое значение этой погрешности:

γ _o = Δ _o/Х_н,

где Х_н – так называемое нормирующее значение измеряемой величины.

ГОСТ 8.401-80 определяет для приборов с равномерной или степенной шкалой, если нулевая отметка находится на краю или вне шкалы, нормирующее значение Х_н равным верхнему пределу диапазона измерений.

Если же нулевая отметка находится посредине шкалы, то Х_н равно протяжённости диапазона измерений (например, для амперметра со шкалой от -30 до +60 А значение Х_н = 60 – (-30) = 90 А.

Значение приведённой погрешности γ _o, выраженное в процентах, используется для обозначения класса точности таких СИ.

Однако полагать, как уже указывалось, что вольтметр класса точности 1,0 обеспечивает во всём диапазоне измерений получение результатов с погрешностью ±1%, – грубейшая ошибка.

В действительности же текущее значение относительной погрешности

γ (х) = Δ _o/x,

т. е. растёт обратно пропорционально х и изменяется по гиперболе.

Таким образом, относительная погрешность γ (х) равна классу точности прибора γ _o лишь на последней отметке шкалы (при х = Х_к).

При х = 0,1Х_к она в 10 раз больше γ_o, а при дальнейшем уменьшении х стремится к бесконечности.

При уменьшении измеряемой величины х до значения абсолютной погрешности нуля Δ _o относительная погрешность результата измерения достигает

γ (х) = Δ _o/x = Δ _o/ Δ _o = 1 = 100%.

Такое значение измеряемой величины, когда х= Δ _o и γ (х) =100%, называется порогом чувствительности СИ.

Отсюда полный диапазон D_п измеряемых величин для любого преобразователя ограничивается снизу порогом чувствительности, а сверху – пределом измерений.

Так как в области малых значений х погрешность измерений очень велика, то рабочий диапазон D_р ограничивают снизу таким значением х, где относительная погрешность измерений γ (х) не превосходит ещё некоторого заранее заданного значения γ_з, равного, например, 4, 10 или 20%.

Таким образом, рабочий диапазон назначается достаточно произвольно и составляет только некоторую часть полного диапазона СИ.

В начальной же части шкалы измерения недопустимы, в чём и заключается отрицательное влияние аддитивной погрешности, не позволяющее использовать один и тот же преобразователь для измерения как больших, так и малых измеряемых величин.

При одновременном присутствии аддитивной и мультипликативной составляющих полоса погрешностей имеет трапецеидальную форму, а текущее значение абсолютной погрешности Δ(х) в функции измеряемой величины х описывается соотношением

, (*)

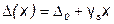где Δ_o – аддитивная, а γ_sх – мультипликативная составляющие абсолютной погрешности.

Если все члены последнего уравнения разделить на предел измерений Х_к, то для приведённого значения погрешности получим

.

Приведённое значение погрешности в начале диапазона (при х=0) обозначим через Δ_o/Х_к =γ_н.

Тогда полученное соотношение примет вид

.

Таким образом, при наличии у СИ и аддитивной, и мультипликативной составляющих погрешности его приведённая погрешность линейно возрастает от γ₀ = Δ_o/Х_к в начале диапазона (при х = 0) до значения γ_к = γ_н + γ_s в конце диапазона (при x = Х_к).

Относительная погрешность результата измерения, исходя из выражения (*), составляет

, (**)

т. е. при x = Х_к она будет равна γ(x) = γ_н + γ_s = γ_к, а по мере уменьшения х возрастает до бесконечности.

Но отличие γ(x) от чисто аддитивной погрешности состоит в том, что заметное возрастание γ(x) начинается тем позже, чем меньше γ_н по сравнению с γ_s.

Такие свойства имеют высокоточные потенциометры постоянного тока, цифровые вольтметры и другие высокоточные приборы.

Формальным отличительным признаком для них является то, что их класс точности, согласно ГОСТ 8.401-80, обозначается не одним, а двумя числами, записываемыми через косую черту, т.е. в виде условной дроби γ_к/γ_н, в числителе которой указывается (в процентах) приведённая погрешность γ_к в конце диапазона измерений, а в знаменателе – приведенная погрешность γ_н в нуле диапазона.