Коррекция проводится с помощью введения в систему специальных корректирующих звеньев с особо подобранной передаточной функцией. Принципиально корректирующие звенья могут включаться либо последовательно с корректируемым звеном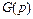 
, либо параллельно ему с образованием местной обратной связи (рисунок 3.1).
В соответствии со способом включения корректирующие звенья делятся на последовательные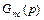 
и параллельные 
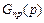. Следует отметить, что при параллельной коррекции основное применение получил именно вариант обратной (отрицательной) связи, а не прямого включения.
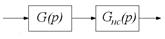
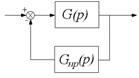
а) последовательное включение б) параллельное включение
Рисунок 3.1 – Способы включения корректирующих звеньев в систему
Корректирующие обратные связи, помимо классификации на отрицательные и положительные, делятся на жесткие и гибкие.
Идеальная жесткая обратная связь осуществляется усилительным звеном с передаточной функцией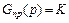 
, идеальная гибкая обратная связь – дифференцирующим звеном с передаточной функцией 
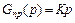, реальная гибкая обратная связь – реальным дифференцирующим звеном с передаточной функцией 
.
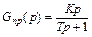В линейных системах оба рассмотренных типа коррекции (последовательный и параллельный) эквивалентны, то есть последовательное звено может быть заменено параллельным, и наоборот, при сохранении неизменными динамических свойств САУ.
Приравняем результирующие передаточные функции, полученные при использовании обоих типов коррекции:
.
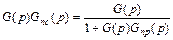Отсюда, например, вытекает следующее выражение для передаточной функций последовательного корректирующего звена, эквивалентного данной обратной связи:
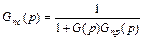. (3.1)
Рассмотрим примеры коррекции свойств САУ.
Пример 17. Охватим жесткой обратной связью интегрирующее звено в составе некоторой САУ (рисунок 3.2).
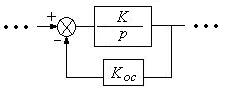
Рисунок 3.2 – Коррекция свойств интегрирующего звена
В результате коррекции передаточная функция звена примет вид
,
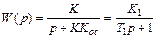где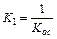 
, 
.
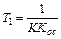Таким образом, при охвате интегрирующего звена жесткой обратной связью оно преобразуется в инерционное звено 1-го порядка.
Пример 18. Охватим жесткой обратной связью инерционное звено 1-го порядка в составе некоторой САУ (рисунок 3.3).
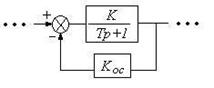
Рисунок 3.3 – Коррекция свойств апериодического звена
В результате коррекции передаточная функция звена примет вид
,
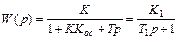где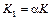 
, 
, 
.
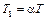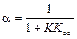Таким образом, в результате охвата апериодического звена жесткой обратной связью его параметры (коэффициент усиления и постоянная времени) изменяются в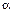 
раз. Уменьшение постоянной времени приводит к ускорению переходных процессов в звене, то есть снижает инерционность или, что равносильно, увеличивает быстродействие.
Передаточная функция эквивалентного последовательного корректирующего звена, согласно выражению (3.1), должна иметь вид
,
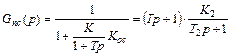где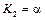 
, 
, .
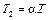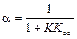Анализ полученного выражения позволяет утверждать, что при последовательной коррекции в рассматриваемом случае необходимо использовать каскадное включение идеального форсирующего звена с параметром Т и инерционного звена 1-го порядка с параметрами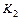 
, 
.
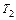