Несколько событий называют несовместными в данном опыте, если никакие два из них не могут появиться вместе.
Теорема сложения утверждает, что если события A и B несовместны, то вероятность появления одного из них, безразлично какого, равна сумме вероятностей этих событий
Следствие.
Вероятность появления одного из нескольких попарно несовместимых событий, безразлично какого, равна сумме вероятностей этих событий.
Во многих реальных ситуациях событие А может произойти вместе с одним из событий Н 1, Н 2, …, Нn, образующих полную группу событий. Эти события называются гипотезами.
Безусловная вероятность P(A) события А вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе.
(2.4)
Данная формула называется формулой полной или средней вероятности.
Пусть имеется полная группа несовместных гипотез Н 1, Н 2, …, Н n. Вероятности этих гипотез до опыта известны и равны соответственно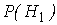 
, 
…, 
. Произведен опыт, в результате которого наблюдается появление некоторого события А. Условные вероятности гипотез после опыта определяются по формуле Бейеса.
. (2.5)
(i = 1, 2,..., n).
Формула Бейеса позволяет переоценить вероятности гипотез после того, как становится известен результат испытания, в итоге которого появляется событие А. Если в результате испытания прибор вышел из строя, гипотезы Н 1 и Н 2 становятся невозможными. Необходимо выяснить и устранить причины отказа прибора.
