В результате испытания группы машин и обработки собранной при этом информации определяют количественные характеристики показателей надежности (среднее значение 
, среднее квадратическое отклонение 
, коэффициент вариации 
и др.).
В дальнейшем значения этих характеристик должны быть перенесены (запланированы) на другие группы машин, работающие в других условиях. Естественно, что изменение количества машин в группе и условий их эксплуатации вызовет изменение количественных характеристик ПН. Хотя эти изменения носят случайный характер, они происходят в определенных границах или в определенном интервале, величина которого зависит от многих факторов, в том числе и от количества машин в группе. Определение границ рассеивания характеристик ПН, следовательно, и определение возможной ошибки их переноса из одних условий в другие является одной из основных задач теории надежности.
Если было проведено наблюдение за 
машинами и на этой основе определено среднее значение ПН , то, как было показано выше, одиночное значение этого же ПН у конкретной машины может в крайних случаях отличаться от 
на величину 
3σ при ЗНР и на величину от 0,1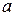 
до 2,5 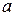при ЗРВ ( 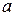- параметр распределения Вейбулла).
Для нормального распределения площадь под дифференциальной кривой, или площадь охвата α, ограниченная протяженностью оси абсцисс 3σ, составляет 0,997, или 99,7%. Следовательно, при таких границах рассеивания в 997 случаях из 1000 значение одиночного ПН будет находиться в интервале значений от -3σ до +3σ.
Таким образом, площадь охвата α равна в долях единицы или в процентах количеству одиночных ПН, числовые значения которых укладываются в границах соответствующего этой площади интервала.
При прочих равных условиях выбранная заранее площадь охвата α характеризует степень доверия расчета и гарантирует вероятность попадания показателя надежности в соответствующий интервал его значений. Поэтому она называется доверительной вероятностью α.
Интервал, в котором при заданной доверительной вероятности α попадают 100 α % от , называют доверительным интервалом 
.
Границы, в которых может колебаться значение одиночного ПН при заданном α, называют нижней доверительной границей 
и верхней доверительной границей 
.
При определении коэффициента 
(количество ) пользоваться интегральным законом нормального распределения и соответственно данными табл. 1 приложения можно только тогда, когда повторность информации N > 100, вследствие чего опытное значение σ будет незначительно отличаться от теоретического. При меньших значениях повторности информации N следует пользоваться законом распределения Стьюдента и коэффициентом , табулированным в табл. 7 приложения.
Рассмотрим уравнения для определения доверительного интервала , доверительных границ и 
и абсолютной ошибки 
для одиночного показателя надежности при законе нормального распределения:
(21)
(22)
(23)
(24)
Анализ расчетных уравнений (21-24) позволяет заметить, что увеличение доверительной вероятности α или повышение степени доверия расчета вызывает увеличение возможной ошибки расчета 
и расширение доверительного интервала. При расчете доверительных границ рассеивания ПН (ГОСТ 17510-72) рекомендуется применять следующие значения доверительных вероятностей: α = 0,80; 0,90; 0,95; 0,99.
Приведем типичный пример расчета доверительных границ одиночного ПН.
Порядок расчета следующий.
Задаемся доверительной вероятностью: α = 0,90.
1. По табл. 7 приложения находим значения коэффициента для α = 0,90 и = 69: = 1,67.
2. По уравнениям (22) и (23) определяем доверительные границы наработок до постановки двигателей в ремонт:
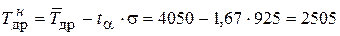мото-ч;
мото-ч.
Доверительный интервал находим по уравнению (24):
мото-ч.
В случае ЗРВ доверительные границы рассеивания одиночного ПН определяют по такой же принципиальной схеме, как и при ЗНР.
Однако вследствие асимметрии дифференциальной функции пользование уравнениями (21)-(24). При относительно больших значениях коэффициента вариации (V =0,6-1,0) может привести к значительным ошибкам.
Доверительные границы рассеивания одиночного ПН при ЗРВ определяются по уравнениям:
(25)
(26)
где 
- квантиль ЗРВ, значение которого находят по таблице 8 приложения (вход в таблицу по величине параметра b и величинам 
или 
).
Если принять, что рассеивание доремонтных ресурсов двигателей согласуется с ЗРВ (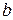
=3,34, 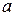=3080 мото-ч, 
=1250 мото-ч), получим:
мото-ч
мото-ч.
В практике чаще всего приходится встречаться с расчетом доверительных границ среднего значения ПН 
.
Расчетная схема и физический смысл доверительных границ при заданной доверительной вероятности α для среднего значения ПН те же, что и для одиночного показателя.
Разница в определении величины среднего квадратического отклонения 
. Связь между и σ установлена в теории вероятностей:
(27)
По аналогии с расчетными уравнениями (21)-(24) для определения рассеивания среднего значения ПН при ЗНР и заданой доверительной вероятности α будет:
абсолютная ошибка:
(28)
- нижняя доверительная граница:
(29)
- верхняя доверительная граница:
(30)
- доверительный интервал:
. (31)
Порядок расчета следующий.
Доверительная вероятность α = 1,67 и коэффициент Стьюдента =1,67 (табл. 7 приложения):
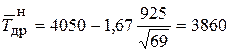мото-ч;
мото-ч;
Из теории надежности известно, что сложение нескольких одинаковых или различных теоретических законов распределения приводит в итоге к закону нормального распределения. Поэтому, когда рассеивание одиночных ПН подчинено ЗРВ, рассеивание средних значений ПН в таких случаях согласуется с законом нормального распределения. Следовательно, доверительные границы рассеивания среднего значения при ЗРВ можно определить по уравнениям (29) и (30).
