При наличии полной информации расчет показателей надежности можно проводить как аналитическим, так и графическим методом на основе дифференциальной или интегральной функции выбранного теоретического закона распределения (ЗНР или ЗРВ). К преимуществам графического метода расчета относится возможность наложения кривых этих функций соответственно на полигон и кривую накопленных опытных вероятностей и на этой основе визуального определения наиболее совпадающего с опытной информацией теоретического закона распределения (ЗНР или ЗРВ), которым и следует пользоваться при дальнейших расчетах показателей надежности.
Известно, что применительно к отказам дифференциальная и интегральная функции характеризуют количество потерявших работоспособность машин или их элементов, или, что практически одно и то же, необходимое количество ремонтных воздействий (устранение эксплуатационных отказов и проведение ремонтов). По дифференциальной функции 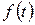 удобно определять количество отказов и, соответственно, количество ремонтных воздействий в любом интервале наработок, а по интегральной функции - суммарное их количество от начала наблюдения за машинами до заданной наработке
удобно определять количество отказов и, соответственно, количество ремонтных воздействий в любом интервале наработок, а по интегральной функции - суммарное их количество от начала наблюдения за машинами до заданной наработке  .
.
При наличии статистического ряда (в случае ЗНР) точки дифференциальной кривой определяют по уравнениям (13) и (14) и по табл. 3 приложения.
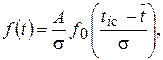 (13)
(13)
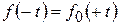 , (14)
, (14)
где 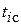 - средние значение показателя надежности в заданном интервале
- средние значение показателя надежности в заданном интервале  (или значение середины интервала статистического ряда).
(или значение середины интервала статистического ряда).
Так, применительно к ресурсам двигателя СМД-14 (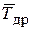 = 4050 мото-ч,
= 4050 мото-ч,  = 925 мото-ч), координатами точек дифференциальной кривой для первого интервала статистического ряда будут:
= 925 мото-ч), координатами точек дифференциальной кривой для первого интервала статистического ряда будут:
- абсцисса - значение показателя надежности в середине первого интервала 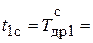 1750 мото-ч;
1750 мото-ч;
- ордината - значение дифференциальной функции в первом интервале (уравнения (13) и (14))
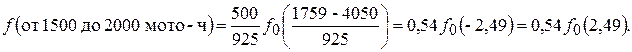 По табл. 3 приложения находим
По табл. 3 приложения находим 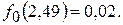 Тогда
Тогда 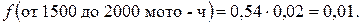
Следовательно, в интервале наработок от 1500 до 2000 мото-ч выйдет из строя (ресурсный отказ) и потребует ремонта около 1% двигателя.
Аналогично для 2-й точки дифференциальной кривой: абсцисса 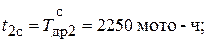 ордината
ордината
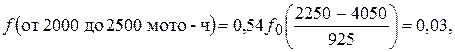
или для 3% двигателей потребуется ремонт в этом интервале наработок и т.д. Результаты расчеты приведены в табл. 4.
Значения интегральной функции 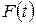 определяют по уравнениям (15) и (16) и данным таблицы 1 приложения.
определяют по уравнениям (15) и (16) и данным таблицы 1 приложения.
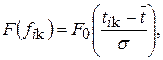 (15)
(15)
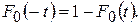 (16)
(16)
Так, в том же расчете по ресурсам двигателя СМД-14 абсцисса 1-й точки интегральной кривой 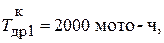 а ордината
а ордината
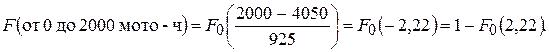
По табл. 2 приложения 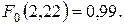 Тогда
Тогда 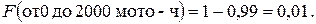 Следовательно, в интервале наработка от 0 до 2000 мото-ч выйдет из строя около 1 % двигателей.
Следовательно, в интервале наработка от 0 до 2000 мото-ч выйдет из строя около 1 % двигателей.
Аналогично для конца второго интервала статистического ряда координаты 2-й точки интегральной кривой будут: абсцисса 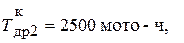 ордината
ордината
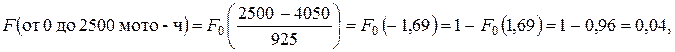 или для 4 % двигателей потребуется ремонт к наработке 2500 мото-ч и т.д. по концам всех интервалов статистического ряда. Результаты расчета приведены в табл. 4.
или для 4 % двигателей потребуется ремонт к наработке 2500 мото-ч и т.д. по концам всех интервалов статистического ряда. Результаты расчета приведены в табл. 4.
Результаты расчета позволяют заключить, что дифференциальная функция 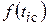 в
в 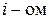 интервале статистического ряда равна разности интегральных функций в конце и начале этого же интервала:
интервале статистического ряда равна разности интегральных функций в конце и начале этого же интервала:
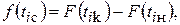 (17)
(17)
где 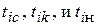 - значения показателей надежности соответственно в середине, в конце и начале
- значения показателей надежности соответственно в середине, в конце и начале  интервала. При законе распределения Вейбулла интегральную функцию
интервала. При законе распределения Вейбулла интегральную функцию 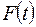 определяют по табл. 9 приложения. Вход в таблицу осуществляется по значению параметра
определяют по табл. 9 приложения. Вход в таблицу осуществляется по значению параметра 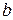 , указанному в верхней строке таблицы, и по величине отношения
, указанному в верхней строке таблицы, и по величине отношения
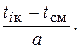 (18)
(18)
Определяем число вышедших из строя двигателей СМД-14 в интервале наработок от 0 до 2000 мото-ч в том случае, если для выравнивания опытной информации (табл. 3) используется ЗРВ. Для конца первого интервала статистического ряда:
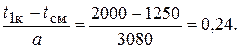
По табл. 9 приложения, проведя интерполирование, найдем 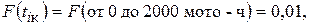 или для 1% двигателей потребуется ремонт в интервале наработок от 0 до 2000 мото-ч.
или для 1% двигателей потребуется ремонт в интервале наработок от 0 до 2000 мото-ч.
Аналогично при наработке, соответствующей концу второго интервала статистического ряда (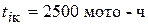 ), получим:
), получим:
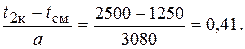
По таблице 9 приложения  (от 0 до 2500 мото-ч) = 0,05, или для 5% двигателей потребуется ремонт в интервале наработок от 0 до 2500 мото-ч.
(от 0 до 2500 мото-ч) = 0,05, или для 5% двигателей потребуется ремонт в интервале наработок от 0 до 2500 мото-ч.
Пользуясь уравнениям (17), определим значение дифференциальной функции 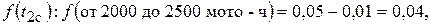 или для 4% двигателей потребуется ремонт в интервале наработок от 2000 до 2500 мото-ч.
или для 4% двигателей потребуется ремонт в интервале наработок от 2000 до 2500 мото-ч.
Результаты расчета интегральных и дифференциальных функций распределения Вейбулла приведены в табл. 4.
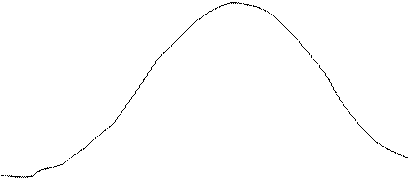
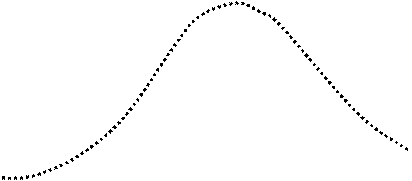
По данным табл. 4 строятся кривые дифференциальной 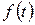 и интегральной
и интегральной 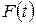 функций ЗНР и ЗРВ и накладываются на полигон (рис. 1) и кривую накопленных опытных вероятностей (рис. 2).
функций ЗНР и ЗРВ и накладываются на полигон (рис. 1) и кривую накопленных опытных вероятностей (рис. 2).
Анализ данных таблицы 4 и графиков (рис. 1 и 2) позволяет сделать рекомендации, имеющие практическое значение:
1. Опытная информация отклоняется от теоретической функции и нуждается в выравнивании при помощи теоретического закона распределения.
2. В интервале значений коэффициента вариации от 0,3 до 0,5 функции ЗРВ незначительно отличаются одна от другой, поэтому визуально трудно выбрать закон распределения для выравнивания опытной информации. В таких случаях рекомендуется выбирать теоретический закон распределения по критерию согласия.
Таблица 4. Сводная таблица опытных и теоретических (ЗНР и ЗРВ) распределений доремонтных ресурсов двигателей
| Интервал, тыс. мото-ч | Опытная вероятность 
| Дифференциальная функция | 
| Интегральная функция | ||||
| ЗНР | ЗРВ | ЗНР | ЗРВ | |||||
| 1,5-2,0 2,0-2,5 2,5-3,0 3,0-3,5 3,5-4,0 4,0-4,5 4,5-5,0 5,0-5,5 5,5-6,0 | 0,03 0,03 0,03 0,20 0,16 0,26 0,14 0,06 0,09 | 0,01 0,03 0,08 0,15 0,20 0,20 0,17 0,09 0,04 | 0,01 0,04 0,10 0,15 0,19 0,20 0,16 0,09 0,04 | 0,03 0,06 0,09 0,29 0,45 0,71 0,85 0,91 1,00 | 0,01 0,04 0,13 0,28 0,48 0,68 0,85 0,94 0,98 | 0,01 0,05 0,15 0,30 0,49 0,69 0,85 0,94 0,98 | ||


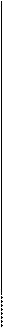





 f(t)
f(t)


 3 1 2
3 1 2
 0,30
0,30










 0,20
0,20
 | |||||
 | |||||
 | |||||





 0,10
0,10

 t см
t см
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||



 4
4
 0,00
0,00
2000 3000 4000 5000 мото-ч.
Рис. 1. Гистограмма (1), полигон (2), дифференциальные кривые закона нормального распределения (3) и закона распределения Вейбулла (4)












 F(t)
F(t)
 ЗНР å Ri
ЗНР å Ri





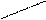
 1,0
1,0

 0,8
0,8
 |
0,6
 |

 0,4
0,4
t см 


0,2
 |

 0,0
0,0
2000 3000 4000 5000 Н, мото-ч.
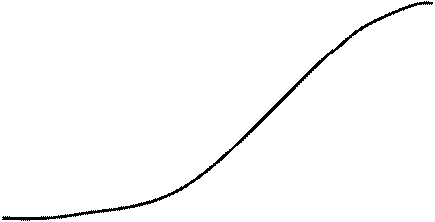
Рис. 2. Кривая накопленных опытных вероятностей ΣР i и интегральная кривая закона нормального распределения (ЗНР)












 F(t)
F(t)
 ЗРВ å Ri
ЗРВ å Ri






 1,0
1,0

 0,8
0,8
 |
0,6
 |

 0,4
0,4
t см 


0,2
 |

 0,0
0,0
2000 3000 4000 5000 Н, мото-ч.
Рис. 3. Кривая накопленных опытных вероятностей ΣР i и интегральная кривая закона распределения Вейбулла (ЗРВ)






