Надежность в период нормальной эксплуатации

В этот период постепенные отказы еще не проявляются и надежность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность.

Длительность периода приработки незначительна по сравнению с общим периодом эксплуатации. Обычно приработка длится от нескольких часов до 100-150 часов. Поэтому для систем, у которых длительность эксплуатации составляет сотни и тысячи часов, этот период не принимается во внимание.

Период нормальной эксплуатации характеризуется тем, что отказ в системе носит случайный и непрогнозируемый характер и, что наиболее важно, частота его наступления не зависит от времени эксплуатации и от возраста изделия, т. е. l =const.

Вероятность безотказной работы в этот период хорошо описывается экспоненциальным законом распределения наработок.

P(t) = 1 - F(t) = е^-^l^t (1)

Q(t) = 1 - е^-^l^t

f(t) = l× е^-^l^t.

Уравнения не зависят от времени эксплуатации объекта, и его надежность для любого времени работы t при известной интенсивности отказов можно непосредственно рассчитать по уравнению (1). Время работы t может быть любым при единственном условии, что интенсивность отказов не будет меняться за это время. При этом предыдущее время эксплуатации объекта не имеет значения. Это положение справедливо для всех устройств, которые прошли надлежащую приработку, но еще не обнаруживают влияния износа, старения и т.п. Важно отметить, что время t в этом случае не должно превосходить длительности нормальной эксплуатации устройства. Отметим некоторые особенности надежности систем при экспоненциальном законе.

Прежде всего, в период нормальной эксплуатации надежность устройства, рассчитываемая во временном интервале Dt=t₂-t₁

P(Dt) ⁼ е^-^l^t² - е^-^l^t¹

всегда одинакова для равных по длительности времен работы, причем совершенно безразлично, какой момент времени принят за начало.

Так, например, надежность для первых 10 часов периода нормальной работы будет ровно такой же, как и для интервала от 990 до 1000 часов, или 540-550 часов и т.п. Например, предположим, что приработанное устройство с 1000-часовым периодом нормальной эксплуатации имеет при определенных условиях постоянную интенсивность отказов Х=0,0001 ч^-1. Надежность устройства для любых 10 часов работы в пределах этих 1000 часов будет следующей:

Р (10) = е ^-0,0001^×¹⁰ = е ^-0,001 = 0,999.

Такова же вероятность безотказной работы устройства в период начальных 10 часов. Но в период от 0 до 990 часов она будет равна:

P (990) = e^- ^0,0001^×⁹⁹⁰ = е ^-0,099=0,90.

Интенсивность отказов полностью определяет надежность устройства. Покажем ее связь с важнейшим параметром надежности средней наработкой на отказ Т ₀. Оно является статистическим параметром и определяется как среднеарифметическое от суммы активной работы всех испытуемых объектов:

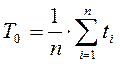
или

Это равенство можно трактовать следующим образом. Средняя наработка на отказ - это время исправной работы всех n изделий в партии, каждое из которых имеет время безотказной работы Т₀.

так как

то можно записать

Средняя наработка на отказ - это время эксплуатации (т.е. при t=T₀), в конце которого вероятность безотказной работы объекта будет равна:

Р(Т₀) = е^-1 = 0,368.

Экспоненциальный закон распределения отказов занимает важное место в расчетах на надежность, т. к. он одинаково хорошо описывает поведение как элементов, так и систем в период их нормальной работы. Он удобен, т. к. единственным параметром l=const (для восстанавливаемых изделий. ω = 1/ Т_О = const) полностью определяется экспоненциальное распределение. Важным достоинством этого распределения является его простота. Если, как это обычно и бывает на практике, l t £ 0,1, то формула для вероятности безотказной работы (1) упрощается в результате разложения в ряд и отбрасывания малых членов:

P(t) = е^-^l = 1 - l t + (l t)² / 2! - (l t)³ / 3!» 1- l t.

На рисунке 2 представлен типичный вид кривых функции надежности, плотности распределения отказов и интенсивности отказов при экспоненциальном законе распределения.

Рисунок 2 – Функция надежности (а), плотности распределения (б) и интенсивности отказов (в) при экспоненциальном законе

Однако надо иметь в виду, что в представленном виде он применим к элементам (и системам) невосстанавливаемым (или восстанавливаемым за пренебрежимо малое время). Если на восстановление затрачивается ощутимое время, то для экспоненциального распределения вероятность появления «r» отказов в системе за суммарное время наработки t определяетсяраспределением Пуассона:

Это уравнение было получено французским математиком Пуассоном для описания распределения независимых случайных событий и называется. Оно широко применяется при описании процессов отказов в случае восстановления системы.

Для восстанавливаемых объектов при экспоненциальном распределении наработок между отказами параметр потока отказа совпадает с интенсивностью отказов, т.е. ω (t) = l.