H.1. Имеется три бесконечно длинных прямолинейных и параллельных проводника A, B и C с текущими в одном направлении токами. Расстояние между проводниками AB = BC = 5 см; IA = IB = I, IC = - 2 I. Найти точку на прямой AC, в которой напряженность магнитного поля, вызванного токами, равна нулю.
●H.2. В однородном магнитном поле с индукцией B = 0,5 Тл находится прямоугольная рамка длиной а = 8 см и шириной b = 5 см, содержащая N = 100 витков тонкой проволоки. Ток в рамке I = 1 A, а плоскость рамки параллельна линиям магнитной индукции. Определить: 1) магнитный момент рамки; 2) вращающий момент, действующий на рамку.
H.3. Ток I течет по тонкому проводнику, который имеет вид правильного n -угольника, вписанного в окружность радиуса R. Найти магнитную индукцию в центре данного контура. Исследовать полученное выражение при 
.
H.4. Ток в 20 А идет по длинному проводнику, согнутому под прямым углом. Найти напряженность магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии 10 см.
●H.5. Определить индукцию магнитного поля в центре проволочной квадратной рамки со стороной a = 15 см, если по рамке течет ток I = 5 A.
H.6. В центре кругового проволочного витка создается магнитное поле H при разности потенциалов U на концах витка. Как нужно изменить приложенную разность потенциалов, чтобы получить вдвое бóльшую напряженность поля в центре витка вдвое большего радиуса, сделанного из той же проволоки?
●H.7. Определить магнитную индукцию в центре кругового проволочного витка радиусом R = 10 см, по которому течет ток I = 1 A.
H.8. Ток I течет по длинному прямому проводнику, сечение кото-рого имеет форму тонкого полукольца радиуса R. Найти индукцию магнитного поля в точке O.
H.9. Однородный ток плотности j течет внутри неограниченной пластины толщины 2 d параллельно ее поверхности. Найти индукцию магнитного поля этого тока как функцию расстояния x от средней плоскости пластины. Магнитную проницаемость всюду считать равной единице.
H.10. По круговому контуру течет ток I = 2 A. При этом в центре контура образуется магнитное поле напряженностью H = 33 A/м. Найти длину проволоки, из которой сделана рамка контура.
●H.11. По прямому горизонтально расположенному проводу пропускают ток I 1 = 10 A. Под ним на расстоянии R = 1,5 см находится параллельный ему алюминиевый провод, по которому пропускают ток I 2 = 1,5 A. Определить, какова должна быть площaдь поперечного сечения алюминиевого провода, чтобы он удерживался незакрепленным. Плотность алюминия ρ = 2,7 г/см3.
H.12. Найти плотность тока как функцию расстояния r от оси аксиально-симметричного потока электронов, если индукция магнитного поля внутри потока зависит от r как B = br α, где b и α – положительные постоянные.
H.13. Требуется получить напряженность магнитного поля H, равную 12,6 э, в соленоиде длиной l = 20 см и диаметром D = 5 см. Найти: 1) число ампер-витков, необходимое для этого соленоида; 2) разность потенциалов, которую необходимо приложить к концам обмотки, если для нее употребляется медная проволока диаметром d = 0,5 мм. Поле соленоида считать однородным.
●H.14. Применяя закон Ампера для силы взаимодействия двух параллельных токов, вывести числовое значение магнитной постоянной μ 0.
H.15. Постоянный ток I = 10 A течет по длинному прямому проводнику круглого сечения. Найти магнитный поток через одну из половин осевого сечения проводника в расчете на один метр.
H.16. В однородном магнитном поле, напряженность которого 1000 э, помещена прямоугольная рамка размером 5 х 10 см. Ее плоскость составляет с направлением поля угол 60о. Найти магнитный поток, пронизывающий рамку.
●H.17. Электрон, обладая скоростью v = 10 Мм/с, влетел в однородное магнитное поле перпендикулярно линиям магнитной индукции. Индукция магнитного поля B = 0,1 мТл. Определить нормальное и тангенциальное ускорения электрона.
H.18. Тонкий провод (с изоляцией) образует плоскую спираль из N = 100 плотно расположенных витков, по которым течет ток I = 8 мА. Радиусы внутреннего и внешнего витков равны a = 50 мм и b = 100 мм. Найти: а) индукцию магнитного поля в центре спирали; б) магнитный мо-мент спирали при данном токе.
H.19. Электрон, ускоренный разностью потенциалов 300 В, движется параллельно прямолинейному длинному проводу на расстоянии 4 мм от него. Какая сила подействует на электрон, если по проводнику пустить ток 5 А?
●H.20. Электрон, обладая скоростью v = 1 Мм/с, влетает в однородное магнитное поле под углом α = 60о к направлению поля и начинает двигаться по спирали. Напряженность магнитного поля H = 1,5 кА/м. Определить: 1) шаг спирали; 2) радиус витка спирали.
H.21. Два протона движутся параллельно друг другу с одинаковой скоростью v = 300 км/с. Найти отношение сил магнитного и электрического взаимодействия данных протонов.
H.22. Протон влетает в однородное магнитное поле под углом 30о к направлению поля и движется по винтовой линии, радиус которой равен 1,5 см. Индукция магнитного поля равна B = 103 Гс. Найти кинетическую энергию протона.
●H.23. Используя теорему о циркуляции вектора B, рассчитать магнитную индукцию поля внутри соленоида (в вакууме), если число витков соленоида равно N и длина соленоида l.
H.24. Квадратная рамка с током I = 0,90 A расположена в одной плоскости с длинным прямым проводником, по которому течет ток I 0 = 5,0 A. Сторона рамки a = 8,0 см. Проходящая через середины противоположных сторон ось рамки параллельна проводу и отстоит от него на расстоянии, которое в η = 1,5 раза больше стороны рамки. Найти: а) амперову силу, действующую на рамку; б) механическую работу, которую нужно совершить для поворота рамки вокруг ее оси на 180о, если токи поддерживают неизменными.
H.25. На соленоид длиной 20 см и площадью поперечного сечения 30 см2 надет проволочный виток. Соленоид имеет 320 витков и по нему течет ток 3 A. Какая средняя ЭДС индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение 0,001 c?
●H.26. Внутри соленоида с числом витков N = 200 с никелевым сердечником (μ = 200) напряженность однородного магнитного поля H = 10 кА/м. Площадь поперечного сечения S = 10 см2. Определить: 1) магнитную индукцию поля внутри соленоида; 2) полный магнитный поток.
H.27. Проводящую плоскость с током поместили во внешнее однородное магнитное поле. В результате индукция магнитного поля с одной стороны плоскости оказалась B 1, а с другой стороны B 2. Найти магнитную силу, действующую на единицу поверхности плоскости в случаях, показанных на рисунках. Выяснить, куда направлен ток в плоскости в каждом случае.
| 
| 
|
H.28. Cоленоид длиной 50 см и площадью поперечного сечения 2 см2 имеет индуктивность 2∙10-7 Гн. При какой силе тока объемная плотность энергии магнитного поля внутри соленоида равна 10-3 Дж/м3?
●H.29. Квадратный проводящий контур со стороной l = 20 см и током I = 10 A свободно подвешен в однородном магнитном поле с магнитной индукцией B = 0,2 Тл. Определить работу, которую необходимо совершить, чтобы повернуть контур на 180о вокруг оси, перпендикулярной направлению магнитного поля.
H.30. Плоский конденсатор, площадь каждой пластины которого S и расстояние между ними d, поместили в поток проводящей жидкости с удельным сопротивлением ρ. Жидкость движется с постоянной скоростью v параллельно пластинам. Система находится в однородном магнитном поле с индукцией B, причем вектор B параллелен пластинам и перпендикулярен к направлению потока. Пластины конденсатора замкнули на внешнее сопротивление R. Какая мощность выделяется на этом сопротивлении? При каком значении R выделяемая мощность будет максимальной? Чему она равна?
H.31. Небольшая катушка с током, имеющая магнитный момент p m, находится на оси кругового витка радиуса R, по которому течет ток I. Найти модуль вектора силы, действующей на катушку, если ее расстояние от центра витка равно x, а вектор p m совпадает по направлению с осью витка.
●H.32. Соленоид диаметром d = 4 см, имеющий N = 500 витков, помещен в магнитное поле, индукция которого изменяется со скоростью 1 мТл/с. Ось соленоида составляет с вектором магнитной индукции угол α = 45о. Определить ЭДС индукции, возникающей в соленоиде.
H.33. Постоянный ток I течет вдоль длинного однородного цилиндрического провода круглого сечения. Провод сделан из парамагнетика с магнитной восприимчивостью χ. Найти: а) поверхностный молекулярный ток 
; б) объемный молекулярный ток 
.
H.34. В однородном магнитном поле, индукция которого 0,25 Тл, находится плоская катушка радиусом 25 см, содержащая 75 витков. Плоскость катушки составляет угол 60о с направлением вектора индукции. Определить вращающий момент, действующий на катушку в магнитном поле, если по витку течет ток 3 А. Какую работу нужно совершить, чтобы удалить катушку из магнитного поля?
H.35. Когда нет перемещения тела, нет и работы в механическом смысле. На что же расходуется энергия, подводимая к электромагниту, когда он "держит" груз?
●H.36. Две гладкие замкнутые металлические шины, расстояние между которыми равно 30 см, со скользящей перемычкой, которая может двигаться без трения, находятся в однородном магнитном поле с индукцией B = 0,1 Тл, перпендикулярном плоскости контура. Перемычка массой m =5 г скользит вниз с постоянной скоростью v = 0,5 м/с. Определить сопротивление перемычки, пренебрегая самоиндукцией контура и сопротивлением остальной части контура.
●H.37. В однородном магнитном поле (B = 0,2 Тл) равномерно с частотой n = 600 мин-1 вращается рамка, содержащая N = 1200 витков, плотно прилегающих друг к другу. Площадь рамки S = 100 см2. Ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции. Определить максимальную ЭДС, индуцируемую в рамке.
H.38. Прямой проводник длиной 1,5 м, движущийся равноускоренно в однородном магнитном поле с начальной скоростью 3 м/c и ускорением 10 м/c2, переместился на расстояние 0,5 м. Найти среднюю ЭДС индукции в проводнике. Индукция магнитного поля равна 0,2 Тл и направлена перпендикулярно скорости движения проводника. Найти также мгновенное значение ЭДС индукции в проводнике в конце перемещения.
●H.39. Длинный соленоид индуктивностью L = 4 мГн содержит N = 600 витков. Площадь поперечного сечения соленоида S = 20 см2. Определить магнитную индукцию поля внутри соленоида, если сила тока, протекающего по его обмотке, равна 6 A.
H.40. К двум произвольным точкам проволочного кольца подведены идущие радиально провода, соединенные с весьма удаленным источником тока. Показать, что индукция магнитного поля в центре кольца равна нулю.
●H.41. Через катушку, индуктивность L которой равна 200 мГн, протекает зависящий от времени ток I = 2cos3 t. Определить: 1) закон изменения ЭДС самоиндукции; 2) максимальное значение ЭДС самоиндукции.
H.42. Электроны, летящие в телевизионной трубке, обладают энергией 12 кэВ. Трубка ориентирована так, что электроны движутся горизонтально с юга на север. Вертикальная составляющая земного магнитного поля направлена вниз, и его индукция B =5,5∙10-5 Тл. В каком направлении будет отклоняться электронный луч? Каково ускорение каждого электрона? На сколько отклонится пучок электронов, пролетев 20 см внутри электронной трубки?
●H.43. Соленоид длиной l = 0,8 м имеет однослойную обмотку из алюминиевого провода массой m = 400 г. Определить время релаксации τ для этого соленоида. Плотность и удельное сопротивление алюминия равны соответственно d = 2,7 г/см3 и ρ = 26 нОм∙м.
H.44. Между рельсами железнодорожного пути включен вольтметр. Над ним с постоянной скоростью проходит поезд. Каковы показания вольтметра при приближении поезда? при нахождении поезда над вольтметром? при удалении поезда? Магнитное поле Земли принять на данном участке однородным, c вертикальной составляющей 
= 5∙10-5 Тл. Ширина колеи 1,2 м. Скорость поезда 60 км/ч.
●H.45. Две катушки намотаны на один сердечник. Индуктивность первой катушки L 1 = 0,12 Гн, второй – L 2 = 3 Гн. Сопротивление второй катушки R 2 = 300 Ом. Определить силу тока I 2 во второй катушке, если за время ∆ t = 0,01 c силу тока в первой катушке уменьшить от I 1 = 0,5 A до нуля.
H.46. Реактивный самолет, имеющий размах крыльев 50 м, летит горизонтально со скоростью 800 км/ч. Определить разность потенциалов, возникающую между концами крыльев, если вертикальная составляющая индукции магнитного поля Земли равна = 5∙10-5 Тл. Можно ли использовать эту разность потенциалов для измерения скорости полета самолета?
●H.47. Обмотка электромагнита, находясь под постоянным напряжением, имеет сопротивление R = 15 Ом и индуктивность L = 0,3 Гн. Определить время, за которое в обмотке выделится количество теплоты, равное энергии магнитного поля в сердечнике.
H.48. Кусок провода длиной l = 2 м складывается вдвое и его концы замыкаются. Затем провод растягивается в квадрат так, что плоскость квадрата перпендикулярна горизонтальной составляющей индукции магнитного поля Земли B || =2∙10-5 Тл. Какое количество электричества пройдет через контур, если его сопротивление R =1 Ом?
●H.49. По круговому контуру радиусом r = 40 см, погруженному в жидкий кислород, течет ток I =1 A. Определить намагниченность в центре этого контура. Магнитная восприимчивость жидкого кислорода χ = 3,4∙10-3.
H.50. При включении магнитного поля, перпендикулярного к плоскости витка радиуса R, по витку протек заряд Q. Какой заряд протечет по витку, если его, при неизменном поле, сложить "восьмеркой", состоящей из двух окружностей, причем радиус меньшей окружности равен R /4? Плоскость "восьмерки" также перпендикулярна магнитному полю.
●H.51. Колебательный контур содержит соленоид (длина l = 5 см, площадь поперечного сечения S 1 = 1,5 см2, число витков N = 500) и плоский конденсатор (расстояние между пластинами d = 1,5 мм, площадь пластин S = 100 см2). Определить частоту ω собственных колебаний контура.
H.52. Металлический диск радиуса R = 25 см вращают с постоянной угловой скоростью ω = 130 рад/с вокруг его оси. Найти разность потенциалов между центром и ободом диска, если: а) внешнего поля нет; б) имеется перпендикулярное к диску внешнее однородное магнитное поле с индукцией B = 5,0 мТ.
●H.53. Колебательный контур содержит катушку с общим числом витков N = 100, индуктивностью L = 10 мкГн и конденсатор емкостью C = 1 нФ. Максимальное напряжение Um на обкладках конденсатора составляет 100 В. Определить максимальный магнитный поток, пронизывающий катушку.
H.54. Квадратная рамка со стороной a и длинный прямой провод с током I находятся в одной плоскости на расстоянии x друг от друга. Рамку поступательно удаляют от тока с постоянной скоростью v. Найти ЭДС индукции в рамке как функцию расстояния x.
●H.55. Колебательный контур состоит из катушки индуктивностью L = 25 мГн, конденсатор емкостью C = 0.1 мкФ и резистора сопротивлением R = 20 Ом. Определить, через сколько полных колебаний амплитуда тока в контуре уменьшится в e раз.
H.56. Металлический стержень массы m может вращаться вокруг горизонтальной оси O, скользя по кольцевому проводнику радиуса a. Схема находится в однородном магнитном поле с индукцией B, направленном перпендикулярно к плоскости кольца. Ось и кольцо подключены к источнику ЭДС, образуя цепь с сопротивлением R. Пренебрегая трением, индуктивностью цепи и сопротивлением кольца, найти, по какому закону должна изменяться ЭДС источника, чтобы стержень вращался с постоянной угловой скоростью ω.
●H.57. Колебательный контур содержит катушку индуктивностью L = 0,1 мГн, резистор сопротивлением R = 3 Ом, а также конденсатор емкостью C = 10 нФ. Определить среднюю мощность, потребляемую контуром, необходимую для поддержания в нем незатухающих колебаний с амплитудным значением напряжения на конденсаторе U m = 2 B.
●H.58. Определить полное сопротивление переменному току (ν = 50 Гц) участка цепи, состоящего из параллельно включенного конденсатора емкостью C = 10 мкФ и резистора R = 50 Ом.
●H.59. В цепи переменного тока с частотой ω = 314 рад/с вольтметр показывает нуль при L = 0,2 Гн. Определить емкость конденсатора.
● 
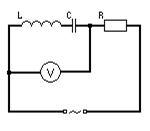H.60. Контур содержит конденсатор емкостью C = 5 нФ, катушку индуктивностью L = 5 мкГн и активное сопротивление R = 0.1 Ом. Определить среднюю мощ-ность, потребляемую колебатель-ным контуром, при поддержании в нем незатухающих гармонических колебаний с амплитудным значением напряжения на конденсаторе UmC = 10 B.
Контрольные вопросы для коллоквиумов,
зачета и экзамена:
1. Электрический заряд. Закон Кулона
2. Электрическое поле. Напряженность поля Е
3. Теорема Остроградского – Гаусса для поля Е (интегральная форма)
4. Теорема Остроградского – Гаусса для поля Е (дифференциальная форма)
5. Примеры применения теоремы Остроградского - Гаусса для поля Е
6. Работа кулоновских сил. Теорема о циркуляции вектора E
7. Энергия и потенциал электростатического поля
8. Связь между напряженностью электростатического по-
ля и его потенциалом
9. Электрический диполь
10. Поле системы зарядов на больших расстояниях
11. Поле и вещество. Поляризация диэлектрика
12. Поляризованность P и связанные заряды
13. Вектор электрического смещения D
14. Условия на границе двух диэлектриков
15. О поле внутри и снаружи проводника
16. Замкнутая проводящая оболочка
17. Общая задача электростатики. Метод изображений
18. Электроемкость. Емкость уединенного проводника
19. Электроемкость. Емкость системы проводников
20. Плоские конденсаторы и их соединения
21. Сферические конденсаторы и их соединения
22. Цилиндрические конденсаторы и их соединения
23. Энергия заряженных проводников и конденсаторов
24. Энергия электрического поля
25. Электрическая энергия системы двух и более тел
26. Энергия электрического поля и силы
27. Постоянный ток. Уравнение непрерывности
28. Закон Ома для участка цепи
29. Закон Ома с точки зрения электронной теории металлов. Зависимость сопротивления от температуры
30. Дифференциальная форма закона Ома
31. Стороннее поле. Электродвижущая сила и напряжение
32. Закон Ома для замкнутой цепи
33. Разветвленные цепи. Правила (законы) Кирхгофа
34. Работа и мощность тока. Закон Джоуля – Ленца
35. Основные понятия и представления о природе магнетизма
36. Сила Лоренца. Поле В
37. Магнитное поле равномерно движущегося заряда
38. Вращающий момент. Индукция и напряженность магнитного поля
39. Магнитное поле тока. Закон Био - Савара – Лапласа
40. Интегральная форма основных законов магнитного
поля
41. Дифференциальная форма основных законов магнитного поля
42. Примеры применения теоремы о циркуляции вектора В
43. Сила Ампера. Закон Ампера
44. Сила взаимодействия параллельных токов
45. Работа по перемещению проводника и контура с током в магнитном поле
46. Намагничение вещества. Намагниченность J
47. Токи намагничения 
.
48. Теорема о циркуляция вектора J
49. Векторы B, J, H. Их взаимная связь и роль в описании магнитных полей
50. Граничные условия для векторов B и H
51. Поле в однородном магнетике
52. Электромагнитная индукция и ее связь с силой Лоренца
53. Электродвижущая сила индукции
54. Явление индукции в неподвижном проводнике. Индукционные токи в сплошных проводниках
55. Закон индукции Фарадея и правило Ленца
56. Электромагнитная индукция и закон сохранения энергии
57. Частные случаи индукции. Явление самоиндукции
58. Частные случаи индукции. Взаимная индукция
59. Энергия электромагнитного поля
60. Основы символьного метода расчета электрических цепей переменного тока
61. Нестационарные состояния (переходные процессы) в цепях переменного тока
62. Связанные колебательные контуры
63. Ток смещения
64. Система интегральных уравнений Максвелла
65. Система дифференциальных уравнений Максвелла
66. Энергия поля и ее поток. Вектор Умова - Пойнтинга
