· Магнитное поле точечного заряда q, движущегося с нерелятивистской скоростью v:
,
· Закон Био-Савара-Лапласа:
· 
, или 
.
· Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:
,
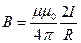где R – расстояние от оси проводника.
· Магнитная индукция в центре кругового проводника с током:
,
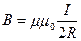где R – радиус кривизны проводника.
· Циркуляция вектора B и теорема Гаусса для него:
, 
,
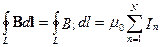где d l – вектор элементарной длины контура, направленной вдоль обхода контура; Bl = B cos α – составляющая вектора B в направлении касательной к контуру L произвольной формы (с учетом выбранного направления обхода); α – угол между векторами B и d l; 
– алгебраическая сумма токов, охватываемых контуром.
· Поток вектора магнитной индукции (магнитный поток) через площадку dS:
dФ S = B dS = BndS.
· Сила Лоренца:
F = q E + q [ v x B ].
· Сила Ампера:
d F = [ j x B ] dV или d F = I [ d l x B ].
· Сила взаимодействия двух прямых бесконечных прямолинейных параллельных проводников с токами I 1 и I 2:
,
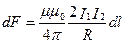где R – расстояние между проводниками; dl – отрезок проводника.
· Сила и момент сил, действующих на магнитный диполь p m = IS n:
, M = [ p m x B ],
где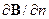 
– производная вектора B по направлению диполя.
· Циркуляция вектора намагниченности J:
,
где 
– суммарный молекулярный ток.
· Вектор H и его циркуляция:
, 
,
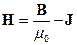где – алгебраическая сумма макроскопических токов, охватываемых контуром.
· Условия на границе раздела двух магнетиков:
B 1 n = B 2 n , H 1τ = H 2τ.
· Для линейных магнетиков, у которых J = κ H:
B = μ 0 μ H, μ = 1+ κ.
· Магнитный поток, создаваемый током в контуре с индуктивностью:
Ф = LI.
· Работа по перемещению проводника с током в магнитном поле:
dA = IdФ,
где dФ – магнитный поток, пересеченный движущимся проводником.
· Работа по перемещению замкнутого контура с током в магнитном поле:
,
где 
– изменение магнитного потока, сцепленного с контуром.
· Закон электромагнитной индукции Фарадея:
.
· ЭДС самоиндукции:
.
· ЭДС взаимной индукции (ЭДС, индуцируемая изменением силы тока в соседнем контуре):
.
· Собственная энергия тока и взаимная энергия двух токов:
, W 12 = L 12 I 1 I 2.
· Объемная плотность энергии магнитного поля:
.
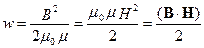