● 
J.1. Сила тока в проводнике равномерно нарастает от I 0 = 0 до I = 5 A в течение времени t = 5 c. Определить заряд, прошедший через проводник.
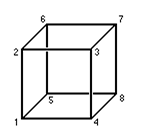
●J.2. Найти сопротивление R проволочного каркаса, имеющего форму куба, при включении его в цепь между точками: а) 1 – 7, б) 1 – 5, в) 1 – 3. Сопротивление каждого из ребер куба равно r.
●J.3. Определить суммарный импульс электронов в прямом проводе длиной l = 500 м, по которому течет ток I = 5 A.
J.4. Зазор между обкладками плоского конденсатора заполнен стеклом с удельным сопротивлением ρ = 100 ГОм∙м. Емкость конденсатора C = 4,0 нФ. Найти ток утечки через конденсатор при подаче на него напряжения U = 2,0 кВ.
●J.5. Вольтметр, включенный в цепь последовательно с сопротивлением R 1, показал напряжение U 1 = 198 В, а при включении последовательно с сопротивлением R 2 = 2 R 1 – U 2 = 180 В. Определить сопротивление R 1 и напряжение в сети, если сопротивление вольтметра Rv = 900 Ом.
●J.6. По алюминиевому проводу сечением S = 0,2 мм2 течет ток I = 0,2 A. Определить силу, действующую на отдельные свободные электроны со стороны электрического поля. Удельное сопротивление алюминия ρ = 26 нОм∙м.
J.7. Металлический шар радиуса a окружен концентрической тонкой металлической оболочкой радиуса b. Пространство между этими электродами заполнено однородной слабо проводящей средой с удельным сопротивлением ρ. Найти сопротивление межэлектродного промежутка. Исследовать полученное выражение при 
.
J.8. Два цилиндрических проводника одинакового сечения, но с разными удельными сопротивлениями ρ 1 и ρ 2, прижаты торцами друг к другу. Найти заряд на границе раздела данных проводников, если в направлении от проводника 1 к проводнику 2 течет ток I.
J.9. Конденсатор емкости C = 400 пФ подключили через сопротивление R = 650 Ом к источнику постоянного напряжения U 0. Через сколько времени напряжение на конденсаторе составит U = 0,9 U 0?
J.10. Два последовательно соединенных источника тока одинаковой ЭДС имеют различные внутренние сопротивления r 1 и r 2, причем r 1 < r 2. Найти внешнее сопротивление R, при котором разность потенциалов на клеммах одного из источников (какого именно?) станет равной нулю.
J.11. Найти ЭДС и внутреннее сопротивление источника, эквивалентного двум параллельно соединенным элементам с ЭДС 
и 
и внутренними сопротивлениями r 1 и r 2.
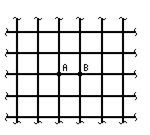
J.12. Имеется безграничная проволочная сетка с квадратными ячейками. Сопротивление каждого проводника между соседними узлами равно r. Найти сопротивление R этой сетки между точками A и B.
J.13. Имеется проводник, у кото-рого известны сопротивление R, не зависящее от темпе-ратуры, и общая теплоемкость C. В момент времени t = 0 его подключили к постоянному напряжению U. Найти зависимость от времени температуры T проводника, считая, что тепловая мощность, отдаваемая им в окружающее пространство q = k (T - T 0), где k – постоянная, T 0 – температура окружающей среды (она же и температура проводника в начальный момент).
J.14. Найти ток, протекающий через сопротивление R 1, если сопротивления R 1 = 10 Ом, R 2 = 20 Ом, R 3 = 30 Ом и потенциалы точек 1, 2, 3 равны соответственно φ 1 = 10 В, φ 2 = 6 В, φ 3 
= 5 В.
J.15. К источнику постоянного тока с внутренним сопротивлением r подключили три одинаковых сопротивления R, соединенных между собой, как показано на рисунке. При каком значении R тепловая мощность, выделяемая на этом участке, будет максимальна?
J.16. Между обкладками плоского конденсатора помещена параллельно им металлическая пластинка, толщина которой составляет η = 0,60 расстояния между обкладками. Емкость конденсатора в отсутствие пластинки C = 20 нФ. Конденсатор подключен к источнику постоянного напряжения U = 100 В. Пластинку медленно извлекли из конденсатора. Найти: а) приращение энергии конденсатора; б) механическую работу, затраченную на извлечение пластинки.
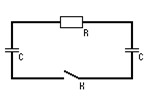
J.17. В схеме емкость каждого конденсатора равна C и сопротивление – R. Один из конденсаторов зарядили до напряжения U 0, а затем в момент t = 0 замкнули ключ K. Найти: а) ток I в цепи как функцию времени t; б) количество тепла, зная зависимость I (t).
J.18. Однородный пучок протонов, ускоренных разностью потенциалов U = 600 кВ, имеет круглое сечение радиуса R 0 = 5,0 мм. Найти напряженность электрического поля на поверхности пучка и разность потенциалов между поверхностью и осью пучка при токе I = 50 мА.
●J.19 Сила тока в проводнике сопротивлением R = 120 Ом равномерно возрастает от I 0 = 0 до I max = 5 A за время τ = 15 c. Определить количество теплоты, выделившееся за это время в проводнике.
● 
J.20. Плотность электрического тока в медном проводе равна 10 A/см2. Определить удельную тепловую мощность тока, если удельное сопротивление меди ρ = 17 нОм∙м.
●J.21. В изображенной на рисунке схеме R 1 = R 2 = R 3 = 100 Ом. Вольтметр показывает U v = 200 В, сопротивление вольтметра R v = 800 Ом. Определить ЭДС батареи, пренебрегая ее сопротивлением.
J.22. Конденсатор, заполненный диэлектриком с проницаемостью ε = 2,1 теряет за время τ = 3,0 мин половину сообщенного ему заряда. Предполагая, что утечка заряда происходит только через диэлектрическую прокладку, вычислить ее удельное сопротивление.
●J.23. Даны четыре элемента с ЭДС 1,5 В и внутренним сопротивлением r = 0,2 Ом. Как нужно соединить эти элементы, чтобы получить от собранной батареи наибольшую силу тока во внешней цепи, имеющей сопротивление R = 0,2 Ом? Определить максимальную силу тока.
J.24. Имеется предназначенный для измерения токов до 10 A амперметр сопротивлением в 0,18 Ом, шкала которого разделена на 100 делений. Какое сопротивление надо взять и как его включить, чтобы этим амперметром можно было измерить силу тока до 100 A? Как изменится при этом цена деления шкалы амперметра?
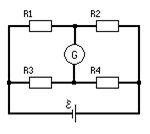
●J.25. На рисунке 
= 2 В, R 1 = 60 Ом, R 2 = 40 Ом, R 3 = R 4 = 20 Ом и R G = 100 Ом. Определить силу тока I G, протекающего через гальванометр.
J.26. Батарея состоит из параллель-но соединенных элементов. При силе тока во внешней цепи 2A полезная мощность равна 7 Вт. Определить число элементов в батарее, если ЭДС каждого элемента 5,5 В, а внутреннее сопротивление 5 Ом.
J.27. Сколько тепла выделится в спирали сопротивлением R при прохождении через нее заряда q, если ток в спирали: а) равномерно убывал до нуля в течение времени ∆ t; б) монотонно убывал до нуля так, что за каждые ∆ t секунд он уменьшался вдвое?
