Связь между векторами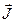 
и 
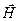. Для некоторых магнетиков зависимость между векторам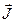и и 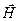имеет линейный характер:
, (97)
где 
- магнитная восприимчивость, безразмерная величина, характеризующая материал магнетика. Магнитная восприимчивость может быть больше и меньше нуля. В соответствии с этим магнетики разделяют на парамагнетики ( >0, 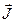↑↑ 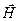) и диамагнетики ( <0, 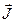↑↓ 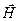). У ферромагнетиков зависимость 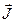(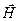) имеет нелинейный характер, и зависит от предыстории образца.
Связь между векторами 
и 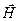. Подставим (91) ® (89), Þ 
, Þ
,Þ
, (98)
где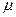 
- магнитная проницаемость среды, которая определяется через следующим образом:
. (99)
У парамагнетиков m >1, у диамагнетиков m <1, причем в обоих случаях мало отличается от 1, поэтому эти магнетики являются слабыми.
Природа диа -, пара - и ферромагнетизма. В грубом приближении электрон в атоме движется по орбите, подобно волчку. В этом случае возникает прецессия орбиты – вращение вектора 
вокруг вектора . Расчет показывает, что для однородного внешнего магнитного поля угловая скорость прецессии одинакова для всех электронов. Вследствие этого возникает дополнительный индуцированный дипольный момент 
~ , что и является причиной диамагнетизма. Если бы атомы обладали собственными магнитными моментами, то они ориентировались бы под действием поля, что приводило бы к появлению магнитного момента 
. Поэтому диамагнитными свойствами обладают атомы, не имеющие собственного магнитного момента.
У парамагнетиков магнитный момент молекул 
, поэтому в магнитном поле они выстраиваются параллельно вектору (и 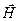). Тепловое движение препятствует этой ориентации, в результате возникает некоторая преимущественная ориентация. Экспериментально установленный закон Кюри показывает, что магнитная восприимчивость парамагнетиков обратно пропорциональна абсолютной температуре
,
где С – постоянная Кюри, зависящая от структуры вещества.
Из-за нелинейности зависимости 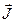(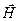) у ферромагнетиков формально вводят 
, причем m имеет физический смысл только для первоначального намагничивания (участок 0®1 на рис.33). Максимальное значение m у ферромагнетиков может быть очень велико, например, у железа m ~ 5000. Зависимость В (Н) называется петлей гистерезиса. При первоначальном увеличении Н индукция магнитного поля В возрастает до некоторой величины (0®1). При последующем уменьшении Н до нуля (1®2) индукция В не спадает до 0; величина этой остаточной индукции 
(0÷2) соответствует остаточному намагничиванию ферромагнетика и объясняет существование постоянных магнитов. Увеличение Н в противоположном направлении (2®3) приводит к полному размагничиванию при напряженности Н 3, называемой коэрцитивной силой, а затем и к перемагничиванию (3®4), т.е. переориентации магнитных моментов в противоположном направлении. При последующем уменьшении Н кривая идет по пути 4®5. При Н =0 (в точке 5) В ¹0. Уменьшение В до нуля происходит при повторном изменении направления и возрастании Н (5®6). Намагничивание на пути 6®1 отличается от первоначального (0®1) и указывает на неоднозначность зависимости 
. Ферромагнетизм нельзя объяснить в рамках классической электродинамики. В ферромагнетике действуют межатомные силы, имеющие квантовую природу, которые ориентируют спиновые моменты электронов в атомах параллельно друг другу. Области с параллельно направленными моментами называются доменами (размер ~ 10-4 см). Во внешнем магнитном поле магнитные моменты доменов ориентируются по полю, значительно увеличивая магнитную индукцию в ферромагнетике. При достаточной величине индукции внешнего поля практически все домены ориентируются вдоль него. При снятии внешнего поля не все домены разориентируются, поэтому для ферромагнитных материалов характерно сохранение остаточной намагниченности.
Условия для векторов и 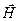на границе раздела магнетиков. Представим на границе двух однородных изотропных магнетиков цилиндр сколь угодно малой высоты (рис.34) и малого сечения S. Тогда по теореме Гаусса для вектора (при стремлении высоты цилиндра к нулю и одновременно к границе): 
, ибо поток через боковую поверхность стремится к 0 вместе с высотой. Отсюда 
, Þ
, (100)
т.е. нормальная составляющая вектора одинакова по обе стороны от границы.
Возьмем вдоль границы прямоугольный контур столь малой длины l, чтобы вдоль него вектор 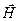мало изменялся (рис.35). Устремим высоту контура к нулю, тогда циркуляция вдоль этого контура сведется к сумме вдоль сторон l и по теореме о циркуляции должна быть равна нулю 
, Þ
. (101)
Это значит: тангенциальная составляющая вектора 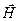одинакова по обе стороны от границы. Очевидно, на границе раздела слабых однородных магнетиков вектор ведет себя аналогично вектору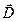 
, а вектор 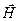- аналогично вектору 
. Поэтому с учетом (98) для остальных составляющих получаем
, 
. (102)
Сопоставление выражений в рамках показывает, что если 
, то при переходе из среды 1 в среду 2 нормальная компонента вектора 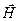уменьшается, а тангенциальная компонента вектора увеличивается. Таким образом, нормальная составляющая вектора 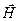и тангенциальная составляющая вектора испытывают скачок при переходе границы раздела магнетиков.
