ќсновн≥ пон€тт€.ƒиференц≥альн≥ р≥вн€нн€ першого пор€дку
ƒиференц≥альн≥ р≥вн€нн€ (ƒ–) застосовують дл€ розвТ€занн€ р≥зних задач математики, природознавства, техн≥ки, економ≥ки.
ќзначенн€ 1. –≥вн€нн€, €ке повТ€зуЇ незалежну зм≥нну  з нев≥домою функц≥Їю
з нев≥домою функц≥Їю 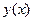 та њњ пох≥дними р≥зних пор€дк≥в, називаЇтьс€ диференц≥альним р≥вн€нн€м.
та њњ пох≥дними р≥зних пор€дк≥в, називаЇтьс€ диференц≥альним р≥вн€нн€м.
ѕриклад 1. а)  ; б)
; б)  ; в)
; в)  .
.
ќзначенн€ 2.Ќайвищий пор€док пох≥дноњ, €ка входить в р≥вн€нн€, називаЇтьс€ пор€дком ƒ–.
–≥вн€нн€ з прикладу 1 а) Ц1-го пор€дку; б)Ц 3-го; в) Ц2-го.
«агальний вигл€д ƒ– 1-го пор€дку
 .
.
якщо його можна розвТ€зати в≥дносно  , то вигл€д ƒ–
, то вигл€д ƒ–
 (1)
(1)
називаЇтьс€ нормальною формою≥ ƒ– першого пор€дку. ѕрипускаЇтьс€, що  - в≥дома функц≥€, €ка задана на де€к≥й множин≥
- в≥дома функц≥€, €ка задана на де€к≥й множин≥  площини
площини  .
.
ќзначенн€ 3. –озвТ€зком (частинним розвТ€зком) ƒ– (1) називаЇтьс€ будь-€ка функц≥€, €ка при п≥дстановц≥ њњ в це р≥вн€нн€ обертаЇ його на тотожн≥сть в≥дносно.–≥вн€нн€, €ке визначаЇ цей розвТ€зок €к не€вну функц≥ю називаЇтьс€ ≥нтегралом (частинним ≥нтегралом) ƒ– (1).√раф≥крозвТ€зку називаЇтьс€ ≥нтегральною кривою.
ѕриклад 2. а) –озвТ€зком ƒ–
 (2)
(2)
Ї функц≥€  , де — Ц дов≥льна стала, оск≥льки п≥сл€ п≥дстановки цього
, де — Ц дов≥льна стала, оск≥льки п≥сл€ п≥дстановки цього  та
та  в р≥вн€нн€ (2) одержимо тотожн≥сть
в р≥вн€нн€ (2) одержимо тотожн≥сть
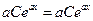 .
.
б)–озвТ€зком ƒ–
 (3)
(3)
Ї функц≥€  , де
, де 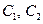 Ц дов≥льн≥ стал≥, оск≥льки
Ц дов≥льн≥ стал≥, оск≥льки  ,
,  та п≥сл€ п≥дстановки цього
та п≥сл€ п≥дстановки цього  в р≥вн€нн€ (3) одержимо тотожн≥сть
в р≥вн€нн€ (3) одержимо тотожн≥сть  .
.
–озвТ€зок (≥нтеграл) ƒ–, €кий залежить в≥д дов≥льних сталих, називаЇтьс€ загальним розвТ€зком (≥нтегралом) ƒ–. ‘ункц≥њ  ,
,  Ї в≥дпов≥дно загальними розвТ€зками ƒ– (2), (3).
Ї в≥дпов≥дно загальними розвТ€зками ƒ– (2), (3).
–озвТ€зок (≥нтеграл) ƒ–, €кий в≥дпов≥даЇ конкретним значенн€м дов≥льних сталих, називаЇтьс€ частинним розвТ€зком (≥нтегралом) ƒ–.
ќзначенн€ 4. –озвТ€зок  ƒ–.(1) задовольн€Ї початков≥й умов≥
ƒ–.(1) задовольн€Ї початков≥й умов≥  , €кщо
, €кщо
 ,
,
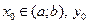 Ц задан≥ числа;
Ц задан≥ числа; 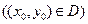 .
.
« геометричноњ точки зору це означаЇ, що ≥нтегральна крива проходить через точку  .
.
ѕриклад 3. –озгл€немо ƒ–  . «розум≥ло, що розвТ€занн€ цього р≥вн€нн€ зводитьс€ до знаходженн€ перв≥сноњ функц≥њ
. «розум≥ло, що розвТ€занн€ цього р≥вн€нн€ зводитьс€ до знаходженн€ перв≥сноњ функц≥њ 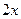 . “ому розвТ€зком буде функц≥€
. “ому розвТ€зком буде функц≥€
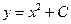 ,
,
–ис.ƒ–_1 | де — Ц дов≥льна стала. «найдемо тепер розвТ€зок, €кий задов≥льн€Ї початков≥й умов≥  . ћаЇмо . ћаЇмо  . .
 .ќтже, розвТ€зок .ќтже, розвТ€зок  зодов≥льн€Ї задан≥й початков≥й умов≥.
–ис.ƒ–_1 ≥люструЇ також той факт, що ƒ– 1-го пор€дку маЇ неск≥нченну множину розвТ€зк≥вЦ с≥мТю (семейство) ≥нтегральних кривих, €к≥ залежать в≥д параметру —, та в даному приклад≥ Ї с≥мТЇю
парабол, €к≥ утворен≥ з параболи зодов≥льн€Ї задан≥й початков≥й умов≥.
–ис.ƒ–_1 ≥люструЇ також той факт, що ƒ– 1-го пор€дку маЇ неск≥нченну множину розвТ€зк≥вЦ с≥мТю (семейство) ≥нтегральних кривих, €к≥ залежать в≥д параметру —, та в даному приклад≥ Ї с≥мТЇю
парабол, €к≥ утворен≥ з параболи  паралельним перенесенн€м уздовж ос≥ ќу
«адачею ош≥ (задачею з початковою умовою) дл€ ƒ–.(1) називаЇтьс€ задача в≥дшуканн€ розвТ€зку ƒ– (1), €кий задовольн€Ї початков≥й умов≥, що задана: паралельним перенесенн€м уздовж ос≥ ќу
«адачею ош≥ (задачею з початковою умовою) дл€ ƒ–.(1) називаЇтьс€ задача в≥дшуканн€ розвТ€зку ƒ– (1), €кий задовольн€Ї початков≥й умов≥, що задана:

|
ћаЇ м≥сце теорема.
“еорема 1.(достатн€ умова Їдиного розвТ€зку задач≥ ош≥). якщо функц≥€ 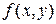 неперервна в област≥
неперервна в област≥  ≥ маЇ в ц≥Їњ област≥ обмежену частинну пох≥дну
≥ маЇ в ц≥Їњ област≥ обмежену частинну пох≥дну  , а точка
, а точка  то задача з початковою умовою маЇ Їдиний розвТ€зок.
то задача з початковою умовою маЇ Їдиний розвТ€зок.
–озвТ€зок задач≥ ош≥ Ї частинним розвТ€зком ƒ– (1).







