Невласні інтеграли
Перейдемо до узагальнення поняття визначеного інтеграла у напрямку, коли: проміжок інтегрування є нескінченним.
Невласний інтеграл по нескінченному проміжку
Нехай функція 
 є інтегрованою на довільному проміжку
є інтегрованою на довільному проміжку  . Покладемо за означенням
. Покладемо за означенням
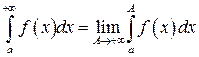 . (11.1)
. (11.1)
Невласний інтеграл  назвемо збіжним, якщо границя існує і скінченна (величина цієї границі приймається за значення невласного інтеграла). У протилежному разі цей невласний інтеграл називається розбіжним.
назвемо збіжним, якщо границя існує і скінченна (величина цієї границі приймається за значення невласного інтеграла). У протилежному разі цей невласний інтеграл називається розбіжним.
Цілком аналогічно визначаються невласні інтеграли:
 ,
,  .
.
Приклад 1. Дослідити на збіжність інтеграли:
1)  ; 2)
; 2) 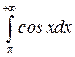 . Розв’язання: 1)
. Розв’язання: 1)  .
.
 Рис.11.1
Рис.11.1
| Оскільки  , то невласний інтеграл збігається і , то невласний інтеграл збігається і  . З геометричної точки зору площа нескінченної криволінійноїтрапеції . З геометричної точки зору площа нескінченної криволінійноїтрапеції  дорівнює дорівнює  (рис. 11.1). (рис. 11.1).
|
б)  . Оскільки границя
. Оскільки границя  не існує (не існує числа до якого прямує
не існує (не існує числа до якого прямує  при
при  ), то невласний інтеграл
), то невласний інтеграл  є розбіжним.
є розбіжним.
Приклад 2. Дослідити на збіжність інтеграл
 . (11.2)
. (11.2)
Розв’язання. Нехай  . Тоді при
. Тоді при 
 та інтеграл (11.2) є
та інтеграл (11.2) є
розбіжним. Якщо  , то
, то  . Звідки при
. Звідки при 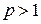 маємо
маємо
 і, таким чином, інтеграл (11.2) збігається, причому
і, таким чином, інтеграл (11.2) збігається, причому
 .
.
У тому разі, коли  , то
, то  та інтеграл (11.2) є розбіжним. Отже, інтеграл (11.2) збігається при
та інтеграл (11.2) є розбіжним. Отже, інтеграл (11.2) збігається при 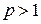 і розбігається при
і розбігається при  .
.
У розібраних вище прикладах відповідь на питання про збіжність або розбіжність інтеграла знаходили за допомогою первісної  підінтегральної функції
підінтегральної функції  . При цьому у разі збіжності невласного інтеграла знаходили і його значення. Проте часто потрібно лише відповісти на питання, збігається чи розбігається невласний інтеграл, а для цього необов’язково знаходити
. При цьому у разі збіжності невласного інтеграла знаходили і його значення. Проте часто потрібно лише відповісти на питання, збігається чи розбігається невласний інтеграл, а для цього необов’язково знаходити  . А саме, наприклад, невласний інтеграл (11.1) від додатної функції
. А саме, наприклад, невласний інтеграл (11.1) від додатної функції  збігається тоді і тільки тоді, якщо при зростанні
збігається тоді і тільки тоді, якщо при зростанні  інтеграл
інтеграл  є обмеженим зверху (див. теорему 4 підрозд. 3.6 посібника). У випадку, якщо інтеграл
є обмеженим зверху (див. теорему 4 підрозд. 3.6 посібника). У випадку, якщо інтеграл  не є обмеженим, то інтеграл (11.1) розбігається (дорівнює
не є обмеженим, то інтеграл (11.1) розбігається (дорівнює  ). На цьому заснована наступна ознака порівняння.
). На цьому заснована наступна ознака порівняння.
Теорема. Нехай  , тоді:
, тоді:
1) інтеграл  є збіжним, якщо інтеграл
є збіжним, якщо інтеграл  збігається;
збігається;
2) інтеграл  є розбіжним, якщо інтеграл
є розбіжним, якщо інтеграл  розбігається.
розбігається.
Наслідок. Якщо для додатних функцій  та
та  існує скінченна границя
існує скінченна границя
 ,
,
то обидва інтеграли  ,
,  збігаються або розбігаються одночасно. Зокрема, якщо
збігаються або розбігаються одночасно. Зокрема, якщо
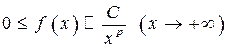 ,
,
то інтеграл  збігається при
збігається при 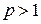 і розбігається при
і розбігається при  .
.
Приклад 3. Дослідити на збіжність інтеграли:
1)  ; 2)
; 2)  .
.
Розв’язання. Відзначимо, що елементарної первісної  в обох випадках не існує.
в обох випадках не існує.
1) Оскільки  , а
, а  збігається, то на підставі теореми збігається і інтеграл
збігається, то на підставі теореми збігається і інтеграл  ;
;
|
 . Отже, на підставі наслідку з теореми випливає, що інтеграл збігається при
. Отже, на підставі наслідку з теореми випливає, що інтеграл збігається при  і розбігається при
і розбігається при  .
.
Збіжний інтеграл  назвемо абсолютно збіжним, якщо збігається інтеграл
назвемо абсолютно збіжним, якщо збігається інтеграл 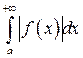 . У випадку, коли інтеграл
. У випадку, коли інтеграл  збігається, а інтеграл
збігається, а інтеграл 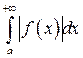 розбігається, будемо казати, що інтеграл
розбігається, будемо казати, що інтеграл  збігається умовно. Слід зазначити, що із збіжності інтеграла
збігається умовно. Слід зазначити, що із збіжності інтеграла 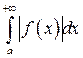 випливає збіжність інтеграла
випливає збіжність інтеграла  .
.
Приклад 4. Дослідити на збіжність інтеграли: а)  ;б)
;б) 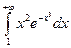 ;в)
;в)  ;
;
г) 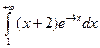 ;д)
;д)  .
.
Розв’язання.а)  =
= 
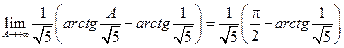 , тобто, збігається.
, тобто, збігається.
а.1) 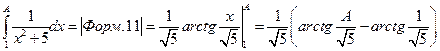
б)  , збігається.
, збігається.
б.1) 
в) 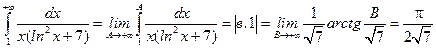 , збігається.
, збігається.
в.1)  .
.
г)  ,збігається.При
,збігається.При
обчисленні границі  була використана формула
була використана формула 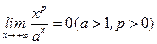 (див. посібник,с.145), зміст якої в тому, що показникова функція
(див. посібник,с.145), зміст якої в тому, що показникова функція  зростає швидше степеневої функції
зростає швидше степеневої функції  .
.
г.1)  =
=
 .
.
д)  ,збігається.
,збігається.
д.1)  .
.






