Значение измеряемой величины А находят по результатам измерений аргументов а 1, …, аi, …, аm, 
связанных с искомой величиной уравнением
(а 1, …, аi, …, аm). (23)
Вид функции f определяется при установлении модели ОИ.
Косвенное измерение при линейной зависимости. Искомая величина А связана с m измеряемыми аргументами уравнением
, (24)
где bi – постоянные коэффициенты.
Предполагается, что корреляция между погрешностями измерений аi отсутствует. Результат измерения А вычисляют по формуле:
, (25)
где 
– результат измерения аi с введенными поправками. Оценку СКО результата измерения σ(А)вычисляют по формуле:
, (26)
где 
– оценка СКО результата измерений .
Доверительные границы Q' (P) случайной погрешности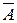 
при нормальном распределении погрешностей
Q' (P) = t (P,nэф)∙ 
, (27)
где t (P,nэф)– коэффициент Стьюдента, соответствующий доверительной вероятности P (обычно 0,95, в исключительных случаях 0,99) и эффективному числу наблюдений nэф, вычисляемому по формуле:
, (28)
где ni – число наблюдений при измерении аi.
Доверительные границы Q (P) НСП результата такого измерения, сумму Q (P) и Q' (P) для получения окончательного значения ∆ (Р)рекомендуется вычислять с использованием критериев и формул (5), (6), (14 – 19), в которых m 1, Qi и σ(x) заменяются соответственно на m, bi ∙ Qi и σ().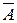
Косвенные измерения при нелинейной зависимости. При некоррелированных погрешностях измерений аi используется метод линеаризации путем разложения функции 
в ряд Тейлора, то есть
, (29)
где 
–отклонение отдельного результата наблюдения аi от 
;
R – остаточный член.
Метод линеаризации допустим, если приращение функции f можно заменить ее полным дифференциалом. Остаточным членом
R = 
(30)
пренебрегают, если
R < 0,8∙ 
, (31)
где σ 
– оценка СКО случайных погрешностей результата измерения . При этом отклонения Δ должны быть взяты из возможных значений погрешностей и такими, чтобы они максимизировали R.
Результат измерения 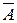вычисляют по формуле:
= 
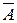. (32)
Оценку СКО случайной составляющей погрешности результата такого косвенного измерения σ(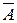) вычисляют по формуле:
σ() =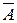 
, (33)
а Q' (P) – по формуле (27). Значение nэф, границы НСП Q (P) и погрешность ∆ (Р) результата косвенного измерения при нелинейной зависимости вычисляют так же, как и при линейной зависимости, но с заменой коэффициентов bi на 
.
Метод приведения (для косвенных измерений с нелинейной зависимостью) применяется при неизвестных распределениях погрешностей измерений аi и при корреляции между погрешностями аi для получения результата косвенного измерения и определения его погрешности. При этом предполагается наличие ряда и результатов наблюдений аij измеряемых аргументов аi. Сочетания аij, полученных в j -м эксперименте, подставляют в формулу (23) и вычисляют ряд значений Aj измеряемой величины A. Результат измерения 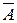вычисляют по формуле:
. (34)
Оценку СКО σ(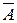) – случайной составляющей погрешности 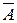– вычисляют по формуле:
, (35)
а Q' (P) – по формуле (22). Границы НСП Q (P) и погрешность ∆ (Р) результата измерения 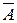определяют описанными выше способами для нелинейной зависимости.
Контрольные вопросы
1. В чем заключается основной постулат метрологии?
2. Что называется результатом однократного измерения?
3. Что называется результатом многократного измерения?
4. Поясните смысл уравнений математических моделей измерения по шкалам отношений и интервалов.
5. Как выражается отсчет?
6. Что вы знаете о свойствах законов распределения вероятности?
7. Расскажите о свойствах математического ожидания.
8. Дайте определение дисперсии. Как определяется среднеквадратичное отклонение?
9. Назовите центральные моменты третьего и четвертого порядков. Как их определяют?
10. С какой ФВ связывают неопределенность случайного числа?
11. Какие основные виды распределений вы знаете?
12. Перечислите способы, исключающие влияющие факторы.
13. Опишите способы обнаружения и исключения грубых погрешностей (промахов)?
14. Что такое доверительный интервал и доверительная вероятность?
15. Что такое нормальное распределение? Какую роль оно играет в метрологии?
16. Для чего используются ситуационные модели?
17. Чем отличаются априорная и апостериорная информации?
18. Сформулируйте второй постулат метрологии.
19. В чем заключается алгоритм обработки результатов однократных измерений с точным оцениванием погрешностей?
20. Как происходит обработка результатов прямых многократных измерений?
21. В чем заключается принципиальная разница в алгоритмах обработки результатов косвенных измерений при линейной и нелинейной зависимостях?
Заключение
Можно выделить три главные функции измерений в народном хозяйстве:
1) учёт продукции народного хозяйства, исчисляющейся по массе, длине, объёму, расходу, мощности, энергии;
2) измерения, проводимые для контроля регулирования технологических процессов и для обеспечения нормального функционирования транспорта и связи;
3) измерения физических величин, технических параметров, состава и свойств веществ, проводимые при научных исследованиях, испытаниях и контроле продукции в различных отраслях народного хозяйства.
От качества измерений зависит эффективность выполнения указанных функций. Повышение точности измерений позволяет определить недостатки тех или иных технологических процессов и устранить эти недостатки. Всё это, в конечном счёте, приводит к повышению качества продукции, экономии энергетических и тепловых ресурсов, а также сырья и материалов.
Эффект, получаемый в народном хозяйстве благодаря использованию измерений, составляет примерно 8…10 руб. на 1 руб. затрат.
Таким образом, измерения являются важнейшим инструментом познания объектов и явлений окружающего мира и играют огромную роль в развитии народного хозяйства.
Качество измерений зависит от уровня развития метрологии как науки: принципов, методов и средств измерений, и др.
Наиболее перспективными направлениями в области повышения качества измерений являются:
1) создание новых научных, технических и нормативно-технических решений, обеспечивающих повышение качества продукции, связанных с измерениями;
2) совершенствование научно-технических, технико-экономических и других видов метрологического обеспечения для повышения эффективности производства современных изделий, качество которых зависит от точности, диапазонности, воспроизводимости измерений физических величин, а также их неизменности на заданном промежутке времени;
3) фундаментальные научные исследования по использованию новых физических эффектов, обеспечивающих создание перспективных методов и средств в области измерений;
4) разработка или совершенствование существующих методов и способов обеспечения единства измерений в области измерений;
5) разработка и внедрение новых эталонов единиц физических величин.
Таким образом, повышение качества измерений является не только метрологической задачей, но и стратегически важным направлением в исследованиях целого ряда естественных и технических наук.
ТЕСТ–КОНТРОЛЬ
1. Какие показатели качества характеризуют свойства безотказности, долговечности, ремонтопригодности и сохраняемости?
а) технологичности;
б) надежности;
в) безопасности;
г) назначения.
2. В чем выражается отличие физической величины от физического свойства?
а) в том, что физическое свойство может быть измерено, а физическая величина нет;
б) в том, что физическая величина может быть измерена, а физическое свойство нет;
в) они ничем не отличаются;
г) в том, что физическое свойство является качественной характеристикой, а физическая величина количественной.
3. На какие группы подразделяют физические величины?
а) главные и второстепенные;
б) качественные и количественные;
в) истинные и условные;
г) основные и производные.
4. Длину, массу, время можно отнести к следующей группе физических величин
а) истинным;
б) производным;
в) основным;
г) качественным.
5. Через какую формулу можно выразить размерность любой физической величины?
а) L α M β∙…;
б) L -α M β A γ∙…;
в) L α T -β∙…;
г) L α M β T γ∙…
6. Показатели размерности физической величины α, β… не могут быть
а) отрицательными;
б) мнимыми;
в) нулевыми;
г) дробными.
7. В каких шкалах используют реперные точки?
а) только в шкалах интервалов;
б) в шкалах порядка и шкалах интервалов;
в) в шкалах порядка и шкалах отношений;
г) во всех перечисленных шкалах.
8. Пользуясь шкалой порядка можно сделать вывод о том:
а) какое значение больше другого и на сколько;
б) какое значение больше другого;
в) какое значение больше другого и во сколько раз;
г) на сколько процентов одно значение больше другого.
9. К какой шкале можно отнести температурную шкалу Кельвина?
а) шкале отношений;
б) шкале интервалов;
в) шкале порядка;
г) к реперной шкале.
10. Все единицы измерения, приведенные ниже, входят в систему единиц СИ
а) ньютон, герц, паскаль, джоуль;
б) длина, герц, атмосфера, джоуль;
в) ньютон, секунда в минус первой степени, бар, эрг;
г) ньютон, герц, метр, бар.
11. Централизованное воспроизведение единиц измерения осуществляется посредством
а) только государственных эталонов;
б) государственных эталонов и вторичных эталонов;
в) рабочими эталонами;
г) эталонными наборами.
12. К какой группе относятся производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, получаемой при прямых измерениях различных сочетаний этих величин?
а) совместные;
б) совокупные;
в) косвенные;
г) прямые.
13. Методы сравнения принадлежат к методам:
а) метод противопоставления, метод непосредственной оценки, дифференциальный метод;
б) метод непосредственной оценки, нулевой метод, дифференциальный метод;
в) метод противопоставления, нулевой метод, метод замещения;
г) метод непосредственной оценки, нулевой метод, метод замещения.
14. На каком методе основаны все показывающие (стрелочные) приборы: вольтметры, амперметры, ваттметры, тахометры, термометры?
а) нулевой метод;
б) метод непосредственной оценки;
в) дифференциальный метод;
г) метод противопоставления.
15. На каком методе измерения основаны аналитические весы?
а) дифференциальный метод;
б) метод непосредственной оценки;
в) метод совпадений;
г) метод противопоставления.
16. В каком методе сравнения с мерой разность между измеряемой величиной и величиной, воспроизводимой другой мерой, измеряют, используя совпадения отметок шкал или периоды сигналов?
а) нулевой метод;
б) метод замещения;
в) метод совпадений;
г) метод противопоставления.
17. Какая из погрешностей по определению зависит от изменения измеряемой величины?
а) абсолютная;
б) систематическая;
в) случайная;
г) динамическая.
18. Сколько составляет приборная погрешность от цены деления шкалы прибора
а) 0,25 от максимальной цены деления;
б) 0,05 от максимальной цены деления;
в) 0,5 от минимальной цены деления;
г) 0,75 от минимальной цены деления.
19. К какому виду погрешностей относится «грубый промах»?
а) случайная погрешность;
б) систематическая погрешность;
в) динамическая погрешность;
г) статическая погрешность.
20. Какую погрешность измеряют всегда в единицах измерения измеряемой величины?
а) статическая;
б) случайная;
в) абсолютная;
г) относительная.
21. Как соотносятся точность измерений a и погрешность b
а) 
;
б) 
;
в) 
;
г)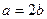 
.
22. Качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях (также отражает влияние случайных погрешностей) это
а) сходимость;
б) воспроизводимость;
в) правильность;
г) достоверность.
23. На какие виды подразделяется контроль объекта?
а) теоретический и эмпирический;
б) активный и пассивный;
в) относительный и абсолютный;
г) статический и систематический.
24. Основная функция эталонов – это…
а) воспроизведение единицы величины;
б) измерение единицы величины;
в) обеспечение единства измерений;
г) подтверждения соответствия измеренной величины.
25. Основной постулат метрологии заключается в том, что
а) отсчет (следовательно, все измерения) является случайным числом;
б) все измерительные приборы имеют погрешность измерений;
в) измерения одной и той же величины различными методами дают разные результаты;
г) приборы могут влиять на измеряемую величину, создавая возмущения.
26. Какой метод применяется, когда измеряемая величина меньше цены деления заданной меры?
а) метод замещения;
б) метод нониуса;
в) дифференцированный метод;
г) нулевой метод.
27. Аналог дисперсии в метрологии?
а) энтропия;
б) квантиль;
в) среднеквадратичное отклонение;
г) эксцесс.
28. Качественным различием измеряемых величин является
а) способ измерения;
б) их размерность;
в) их погрешность;
г) их величина.
29. Условия необходимые для обеспечения единства измерений?
а) узаконенная система единиц;
б) наличие рабочих эталонов;
в) наличие средств измерений;
г) неопределенность измерений.
30. Математическая модель величины – это
а) это описание величины математическими средствами;
б) это универсальный объект измерения;
в) это величина, которая отражает изменение объекта измерения и среду с течением времени;
г) это значение величины.
31. Наиболее универсальной математической моделью детерминированной величины являются
а) ряд Тейлора;
б) ряд Фурье;
в) преобразование Лапласа;
г) ряд Котельникова.
32. Математическое ожидание определяется по формуле
а) 
; б) 
;
в) 
; г) 
.
33. Когда каждое из чисел подвергается обработке
а) сразу же после его получения в процессе моделирования;
б) после моделирования;
в) параллельно ему (при условии, что характеристики моделируемого случайного объекта не известны);
г) параллельно, после вычисления, получения или обработки первого числа.
34. Какой способ измерений применяют для исключения прогрессирующего влияния какого-либо фактора, являющегося линейной функцией времени?
а) полных измерений;
б) абсолютных измерений;
в) симметричных измерений;
г) равноточных измерений.
35. Поправки делятся на …
а) абсолютные и относительные;
б) равноточные и неравноточные;
в) статические и динамические;
г) аддитивные и мультипликативные.
36. Возмущающий фактор – это…
а) влияние средства измерений на измеряемую величину;
б) некомпетентность оператора;
в) погрешность измерений;
г) ошибка измерения.
37. Для математического описания ситуаций, в которых по какой-либо причине не хватает нужной количественной информации используются
а) статические модели;
б) ситуационные модели;
в) неравенства Чебышева;
г) нормальный закон распределения вероятности.
38. Центральная предельная теорема теории вероятности утверждает, что результат измерений подчиняется
а) правилу трех сигм;
б) нормальному закону распределения вероятности;
в) второму постулату метрологии;
г) функции Лапласа.
39. априорная информация - это…
а) информация, полученная путем прямых измерений;
б) дефицит информации о значении измеряемой величины;
в) информация, которой располагали до измерения;
г) количество информации, получаемое в результате измерений.
40. Несмещенность среднего значения результата измерения относительно значения измеряемой величины обеспечивает
а) точность измерений;
б) вероятность того, что результат однократного измерения окажется за пределами доверительного интервала;
в) правильность измерения;
г) равноправность измерений.
41. Многократное измерение одной и той же величины постоянного размера производится при повышенных требованиях к …
а) точности измерения;
б) правильности измерения;
в) несмещенности измерения;
г) единству измерений.
42. Значения отсчета xi, имеющие одинаковую дисперсию называются
а) абсолютными;
б) относительными;
в) неравноточными;
г) равноточными.
43. Как называется точечная оценка числовых характеристик, которая сходится по вероятности к оцениваемой числовой характеристике?
а) несмещенная;
б) состоятельная;
в) эффективная;
г) равноточная.
44. Как называется точечная оценка числовых характеристик, математическое ожидание которой равно оцениваемой числовой характеристике?
а) несмещенная;
б) состоятельная;
в) эффективная;
г) равноточная.
45. Какие методы обработки данных применяют, если закон распределения вероятности результата измерения незначительно отличается от нормального?
а) математические;
б) статические;
в) робастные;
г) экспериментальные.
