Обработку результатов в этом случае рекомендуется начать с проверки на отсутствие промахов (грубых погрешностей). Промах – это результат xn отдельного наблюдения, входящего в ряд из n наблюдений, который для данных условий измерений резко отличается от остальных результатов этого ряда. Если оператор в ходе измерения обнаруживает такой результат и достоверно находит его причину, он вправе его отбросить и провести (при необходимости) дополнительное наблюдение взамен отброшенного.
При обработке уже имеющихся результатов наблюдений произвольно отбрасывать отдельные результаты нельзя, так как это может привести к фиктивному повышению точности результата измерения. Поэтому применяют следующую процедуру. Вычисляют среднее арифметическое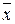 
по формуле (12).
Затем вычисляют оценку СКО результата наблюдения σ(x) по формуле (11).
Находят отклонение VП предполагаемого промаха xn от :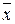
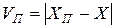. (20)
По числу всех наблюдений n (включая xП) и принятому для измерения значению P (обычно 0,95) по любому справочнику по теории вероятностей находят z (P.n) – нормированное выборочное отклонение нормального распределения.
Если VП < z∙σ (x), то наблюдение xП не является промахом; если VП ≥ z∙σ (x), то xП – промах, подлежащий исключению. После исключения xП повторяют процедуру определения 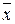и σ (x) для оставшегося ряда результатов наблюдений и проверки на промах наибольшего из оставшегося ряда отклонений от нового значения (вычисленного исходя из n – 1.
За результат измерения принимают среднее арифметическое 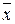результатов наблюдений xi. Погрешность 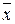содержит случайную и систематическую составляющие. Случайную составляющую, характеризуемую СКО результата измерения, оценивают по формуле:
. (21)
Принадлежность результатов наблюдений xi к нормальному распределению при 
, легко проверить, применив правило 3σ: если отклонение от 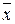не превышает 3σ, то случайная величина распределена нормально. Доверительные границы случайной погрешности результата измерения при доверительной вероятности Р находят по формуле:
Q' (P) = t (P,n)∙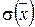 
, (22)
где t – коэффициент Стьюдента.
Доверительные границы Q (P) НСП результата измерения с многократными наблюдениями определяют точно так же, как и при измерении с однократным наблюдением – по формулам (5) и (6).
Суммирование систематической и случайной составляющих погрешности результата измерения при вычислении ∆ (Р) рекомендуется осуществлять с использованием критериев и формул (14 – 19), в которых при этом σ (x) заменяется на .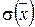
