За результат измерения в этом случае принимают результат однократного наблюдения х (с введением поправки, если она имеется), используя предварительно полученные (например, при разработке МВИ) данные об источниках, составляющих погрешность.
Доверительные границы НСП (неисключенная систематическая погрешность) результата измерения Q (P) вычисляют по формуле:
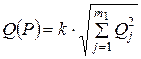 , (5)
, (5)
где, k – коэффициент, определяемый принятой Р и числом m 1 составляющих НСП: Q (Р) – найденные нестатическими методами границы j- й составляющей НСП (границы интервала, внутри которого находится эта составляющая, определяемые при отсутствии сведений о вероятности ее нахождения в этом интервале). При Р = 0,90 и Р = 0,95 k равен 0,95 и 1,1 соответственно при любом числе слагаемых m 1. При Р = 0,99 значение k следующие (табл.5):
Таблица 5
| m 1 | k | m 1 | k |
| 5 и более | 1,45 | 1,30 | |
| 1,40 | 1,20 |
Если составляющие НСП распределены равномерно и заданы доверительными границами Q (Р), то доверительную границу НСП результата измерения вычисляют по формуле:
 , (6)
, (6)
где k и kj – те же, что и в предыдущем случае, коэффициенты, соответствующие доверительной вероятности Р и Pj соответственно;
m 1– число составляющих НСП.
Среднее квадратическое отклонение (СКО) результата измерения с однократным наблюдением вычисляют одним из следующих способов:
Если в технической документации на СИ или в МВИ указаны нормально распределенные составляющие случайной погрешности результата наблюдения (инструментальная, методическая, из-за влияющих факторов, оператора и т.д.), то СКО вычисляют по формуле:
 , (7)
, (7)
где m 2 – число составляющих случайной погрешности;
σi – значения СКО этих составляющих.
Доверительную границу случайной погрешности результата измерения Q' (P) в этом случае вычисляют по формуле:
Q' (P) = zP /2∙σ(x), (8)
где zP /2 – значение нормированной функции Лапласа в точке P /2 при доверительной вероятности P (табл. 6).
Таблица 6
| P | zP /2 | P | zP /2 |
| 0,90 | 1,65 | 0,97 | 2,17 |
| 0,95 | 1,96 | 0,98 | 2,33 |
| 0,96 | 2,06 | 0,99 | 2,58 |
· Если в тех же документах случайные составляющие погрешности результата наблюдения представлены доверительными границами Qi' (P) при одной и той же доверительной вероятности P, то доверительную границу случайной погрешности результата измерения с однократным наблюдением при доверительной вероятности вычисляют по формуле:
Q' (P) = 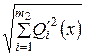 . (9)
. (9)
· Если случайные составляющие погрешности результата наблюдения определяют предварительно в реальных рабочих условиях экспериментальными методами при числе наблюдений ni < 30, то
Q' (P) = t ∙ 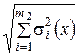 , (10)
, (10)
где t – коэффициент Стьюдента, соответствующий наименьшему числу наблюдений n min из всех ni, значение которого можно найти в любом справочнике по теории вероятностей;
σ(x) – оценки СКО случайных составляющих погрешности результата наблюдения, определяемых по формуле:
σ(x) =  , (11)
, (11)
где 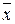 – среднее арифметическое результатов наблюдений xi, определяемое по формуле:
– среднее арифметическое результатов наблюдений xi, определяемое по формуле:
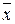 =
= 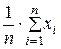 . (12)
. (12)
Если в эксперименте невозможно или нецелесообразно определить СКО составляющих случайной погрешности и определено сразу суммарное СКО, то в формуле (8) m 2 = 1.
· Если случайные составляющие погрешности результата наблюдений представлены доверительными границами Q' (Pi), соответствующими разным вероятностям Pi, то сначала определяют СКО результата измерения с однократным наблюдением по формуле:
σ(x) = 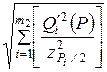 , (13)
, (13)
где  – значения функции Лапласа.
– значения функции Лапласа.
Затем вычисляют Q' (P) по формуле (8).
Для суммирования систематической и случайной составляющих погрешностей рекомендуется следующий способ:
Если
 , (14)
, (14)
то НСП 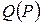 пренебрегают и окончательно принимают Q' (P) за погрешность результата измерения ∆ (Р) при доверительной вероятности Р.
пренебрегают и окончательно принимают Q' (P) за погрешность результата измерения ∆ (Р) при доверительной вероятности Р.
Если
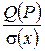 > 0,8, (15)
> 0,8, (15)
то пренебрегают случайной погрешностью и принимают ∆ (Р) = 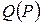 .
.
Если
0,8 ≤ 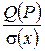 ≤ 0,8, (17)
≤ 0,8, (17)
то доверительную границу погрешности результата измерений вычисляют по формуле:
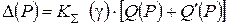 , (18)
, (18)
 ;
;  , (19)
, (19)






