Стандартное отклонение для оценки обозначается Se и рассчитывается по формуле среднеквадратичного отклонения:
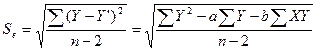 .
.
Величина стандартного отклонения характеризует точность прогноза.
Вариант 5. Возвращаясь к данным нашего примера, рассчитаем значение Se:
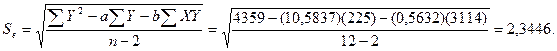
Предположим, необходимо оценить значение Y для конкретного значения независимой переменной, например, спрогнозировать объем продаж при затратах на рекламу в объеме 10 тыс. долл. Обычно при этом также требуется оценить степень достоверности результата, одним из показателей которого является доверительный интервал для Y.
Граница доверительного интервала для Y при заданной величине X рассчитывается следующим образом:
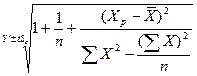
где Хp – выбранное значение независимой переменной, на основе которого выполняется прогноз. Обратите внимание: t – это критическое значение текущего уровня значимости. Например, для уровня значимости, равного 0,025 (что соответствует уровню доверительности двухстороннего критерия, равному 95%) и числа степеней свободы, равного 10, критическое значение t равно 2, 228 (см. Приложение II). Как можно увидеть, доверительный интервал – это интервал, ограниченный с двух сторон граничными значениями предсказания (зависимой переменной).
Вариант 6. Для нашего примера расходов на рекламу в размере 10 тыс. долл. интервал предсказания зависимой переменной (объема продаж) с уровнем доверительности в 95% находится в пределах [10,5951; 21,8361]. Его границы определяются следующим образом (обратите внимание, что в Варианте 2 Y'=16,2156):
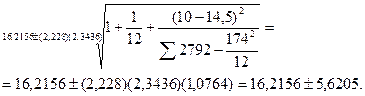
Из приведенного расчета имеем: для заданных расходов на рекламу в объеме 10 тыс. долл., объем продаж изменяется в диапазоне от 10,5951 до 21,8361 тыс. долл. При этом: 10,5951=16,2156-5,6205 и 21,8361=16,2156+5,6205.






