Метод наименьших квадратов. Метод наименьших квадратов широко используется в регрессионном анализе для расчета значений коэффициентов в уравнении регрессии

Метод наименьших квадратов широко используется в регрессионном анализе для расчета значений коэффициентов в уравнении регрессии. Для регрессионного анализа используются данные всех наблюдений и ищется прямая наилучшего согласия с помощью метода наименьших квадратов. На рисунке 16.1 показано регрессионное взаимодействие.

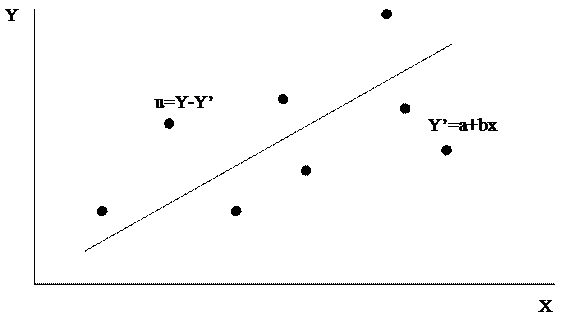
Рисунок 16.1 – Схема построения линии наилучшего приближения

по методу наименьших квадратов

Чтобы пояснить метод наименьших квадратов, определим невязку (отклонение) как разницу между наблюдаемым значением и его оценкой и обозначим ее через u: u=Y-Y’, где Y – наблюдаемое значение зависимой переменной; Y’ – расчетное значение зависимой переменной, выполняемое по формуле: Y’=a+bX.

Согласно критерию наименьших квадратов прямая наилучшего согласия должна располагаться таким образом, чтобы сумма квадратов невязок (на рис. 16.1 это расстояние по вертикали от точек, соответствующих наблюдениям, по прямой) были минимальной, т.е. .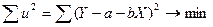

Для нахождения минимума продифференцируем и приравняем нулю производную. Получим:

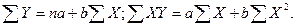
Решая уравнения относительно b и a, получаем:

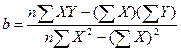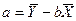, , где , .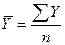

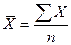Вариант 1. Чтобы показать, как рассчитываются значения b и a, используем данные табл. 16.1. Все расчеты приведены ниже таблицы.

Таблица 16.1 – Объемы продаж и затрат на рекламу

Из таблицы следует: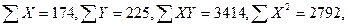

.

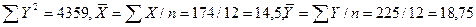Подставляя полученные значения в вышеприведенные формулы, получаем:

;

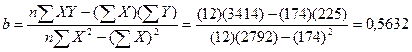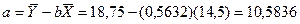
Тогда можно записать: .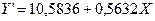

Вариант 2. Предположим, что расходы на рекламу в следующем периоде также составили 10 тыс. долл. Предполагаемый объем продаж следующего периода (в тыс. долл.) рассчитывается:

.
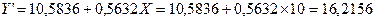