Преимущества и недостатки

Скользящее среднее просто рассчитывается и легко понимается. Однако имеются два ограничения:

1) необходимо хранить большой объем данных от периода к периоду;

2) все данные - и прошлых периодов, и текущие - взвешиваются с одинаковыми коэффициентами. Вероятно, стоит присваивать данным текущего периода больший весовой коэффициент, если они важнее.

Метод экспоненциального сглаживания свободен от указанных недостатков.

Экспоненциальное сглаживание

Экспоненциальное сглаживание - популярный метод краткосрочного прогнозирования. Использует взвешенное среднее данных прошлых периодов как основу для прогнозирования. При этом большие весовые коэффициенты присваиваются более поздним данным и меньшие - данным наблюдений прошлых периодов. Считается, что будущее больше зависит от близкого прошлого и меньше - от удаленных по времени наблюдений.

Метод эффективен в том случае, когда допускаются случайные изменения и отсутствуют колебания сезонного характера. К недостатку метода относится то, что он не учитывает отраслевые и экономические факторы, такие как рыночные условия, цены, эффект от действий конкурентов.

Модель

Формула экспоненциального сглаживания: 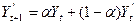, где Y'_t+1 – среднее прогнозное значение будущего периода, рассчитываемое с учетом экспоненциального сглаживания; Y_t - фактические данные текущего периода; Y’ _t - прогнозное значение показателя текущего периода; α - постоянная сглаживания.

Чем выше значение постоянной сглаживания, тем больший вес присваивается самым последним наблюдениям.

Вариант 3. Ниже показаны данные по объемам продаж.

Номер периода	Фактический объем продаж, тыс. долл.,Y

 

Чтобы инициировать процесс экспоненциального сглаживания, необходимо сделать первоначальный прогноз:

- первых фактических наблюдений;

- среднего значения для фактических данных нескольких периодов.

В рассматриваемом случае в качестве первоначального прогнозируемого значения Y’₇ будем использовать усредненное значение на основе данных 6 периодов и постоянную сглаживания α = 0,40.

Тогда

.

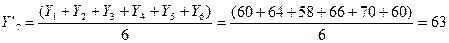Обратите внимание, Y₇=70. Тогда Y’₈ рассчитывается по следующей формуле:

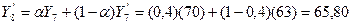
Аналогично:

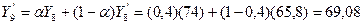
и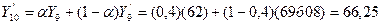

Используя ту же процедуру, можно рассчитать значения 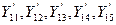. В зависимости от положительной или отрицательной величины отклонения между фактическим и спрогнозированным значением, человек, выполняющий прогноз, может использовать большее или меньшее значение α и, таким образом, достаточно быстро подстроить прогноз В соответствии с разбросом в выборке данных.

Например, если прогноз медленно реагирует на возросший объем продаж (т. е. отклонение - отрицательная величина), необходимо выбирать большее значение. Для практических целей можно найти оптимальное значение а с помощью минимизации дисперсии (s²):

,

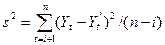где i - количество наблюдений, которые участвуют в расчете первоначального прогноза (в нашем примере i = 6).

В нижеследующей таблице сравниваются фактический объем продаж и прогнозируемый объем, полученный с помощью метода экспоненциального сглаживания.

Сравнение фактических и прогнозируемых значений объема продаж, тыс. долл

Номер периода	Фактические продажи, Yt	Прогнозируемые продажи Yt’	Отклонение	Квадрат отклонения,
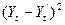
		63,0	7,0	49,0
		65,80	8,20	67,24
		69,08	-7,08	50,13
		66,25	7,75	60,06
		69,35	-1,35	1,82
		68,81	-2,81	7,90
		67,69	-7,69	59,14
		64,61	1,39	1,93
		65,17	-3,17	10,05
				307,27

 

В нашем случае: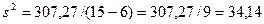

Задачей является выбор значения α, минимизируюшего величину s², представляющую собой усредненную сумму квадратов отклонений между фактическими и прогнозируемыми значениями соответствующих периодов.