Нехай відоме значення функції f (x) у точці х 0, тобто f (x 0). Знайти значення f (x 0 + D х).
Очевидно, що має місце рівність f (x0 + Dx) = f (x0)+ Df.
У наближених обчисленнях, якщо D х мале, то приріст D f у точці х 0 замінюється диференціалом dy у цій точці, тобто f ¢(x 0)D x, і тоді дістаємо наближену рівність
f (x 0 + D x)» f (x 0) + f ¢(x 0)D x.
Якщо позначити х = х 0 + D х, матимемо
f (x)» f (x 0) + f ¢(x 0)(x – x 0).
Запишемо формулу наближених обчислень для деяких функцій:
sin (x0 + Dx)» sin x0 + cos x0·Dx;
cos (x0 + Dx)» cos x0 – sin x0·Dx;
;
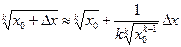ln (x0 + Dx)» ln x0 +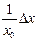 
;
;
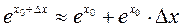arcsin (x0 + Dx)» arcsin x0 +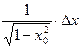 
.
Приклад. Обчислити наближено 
.
Розв’язання. За умовою потрібно знайти значення функції f (x) = =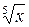 
при х = 34. Вибираємо точку х 0 так, щоб у ній легко можна було б обчислити функцію, і вона була б близькою до точки х. У даному випадку х 0 = 32, f (32) = 
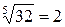, тоді D х = 34 – 32 = 2 і, таким чином,
; 
; 
.
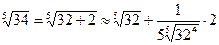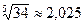Похідні і диференціали вищих порядків
