Тема: Диференціювання неявних і параметрично заданих функцій. Рівняння дотичної і до кривої
Диференціювання неявно заданих функцій
Нехай функція y = y (x) задана неявно рівнянням F (x, y) = 0. Для знаходження похідної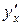 
цієї функції потрібно продиференціювати обидві частини заданого рівняння по x, вважаючи y функцією від x, а потім з одержаної рівності виразити 
.
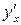Приклад. Знайти 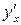, якщо y (x) визначається рівнянням:
y = cos (x + y).
Розв’язання.
; 
;
; 
;
; 
.
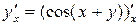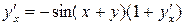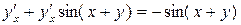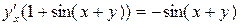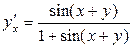З наведеного прикладу видно, що похідна неявної функції виражається через незалежну змінну і саму функцію.
Диференціювання параметрично заданих функцій
Нехай функція y = y (x) задана параметрично рівняннями
(T 0 £ t £ T 1),
де x (t), y (t) – диференційовні функції від t. Потрібно знайти похідну функції y = y (x), тобто .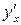
Похідну функції, заданої параметрично шукають за формулою 
.
Приклад. Знайти 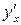, якщо x = R (t – sin t), y = R (1 – cos t).
Розв’язання. Знаходимо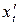 
та 
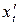: = R (1 – cos t), = R sin t. Тепер
.
