Формула повного приросту функції

Нехай в точці х функція y = f (x) диференційовна, тобто має по­хідну у ¢(х) = f ¢(x). Тоді згідно з означенням похідної, маємо: .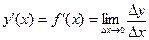

Існування границі означає, що при малих значеннях D х має місце відношення

,

де a(D х) – функція від D х, нескінченно мала при D х ® 0 (a(D х) ® 0 при D х ® 0). Таким чином, маємо

D у = у ¢(х)·D х + a(D х)·D х.

Цей вираз називають формулою повного приросту функції. З нього випливає, що D у є сума двох доданків. Перший з них у ¢(х)·D х є добуток сталої у ¢(х) = А на нескінченно малу величину D х (лінійний відносно D х) і має той же порядок, що й D х:

.

Другий доданок a(D х)D х при D х ® 0 є нескінченно малою вищо­го порядку порівняно з D х:

,

так що a(D х)D х = о (D х). Тому формулу (1) можна подати у вигляді:

D у = у ¢(х)D х + о (D х), або D у = А D х + о (D х). Доданок А D х називається головною частиною приросту функ­ції D у. Головна частина приросту функції еквівалентна при D х ® 0 при­росту функції: А D х ~ D у, оскільки їх різниця D у – А D х = о (D х) є нескінченно малою вищого порядку порівняно з D х.