Рівняння дотичної і нормалі до кривої

Нехай рівняння y = f (x) є рівняння деякої кривої, яка в точці M ₀(x ₀, f (x ₀)) має дотичну, тобто функція y = f (x), диференційовна при x = x ₀. Проведемо через точку M ₀(x ₀, f (x ₀)) кривої y = f (x) дотичну M ₀ T.

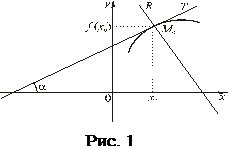
Означення. Нормаллю (рис.1) до кривої y = f (x) називається пряма, яка проходить через точку дотику M ₀(x ₀, f (x ₀)) перпендикуляр­но до дотичної в цій точці (пряма M ₀ R).

Рівняння дотичної шукаємо у вигляді:

y – y ₀ = k (x – x ₀),

де k = tg a – кутовий коефі­цієнт прямої. Із геометричного змісту похідної відомо, що
tg a = f ¢(x ₀). Отже, рівняння до­тичної до кривої y = f (x), прове­де­ної в точці M ₀(x ₀, f (x ₀)), має вигляд

y – y ₀ = f ¢(x ₀)(x – x ₀), де y ₀ = f (x ₀).

Як відомо, кутові коефіцієнти взаємно перпендикулярних пря­мих зв’язані рівністю k ₁· k ₂ = – 1. Тому кутовий коефіцієнт нормалі до кривої, проведеної в точці M ₀(x ₀, f (x ₀)), дорівнює і рів­няння нормалі має вигляд: .

Приклад. Скласти рівняння дотичної і нормалі до кривої y = x ³ в точці M ₀(1, 1).

Розв’язання. Рівняння дотичної має вигляд:

y – y ₀ = f ¢(x ₀)(x – x ₀),

де x ₀ = 1, y ₀ = 1. Маємо y ¢ = (x ³)¢ = 3 x ². Тоді f ¢(x ₀) = f ¢(1) = 3. Отже, шу­кане рівняння дотичної:

y – 1 = 3(x – 1); 3 x – y – 2 = 0.

Рівняння нормалі має вигляд ,

тобто , або x + 3 y – 4 = 0.