Два рівняння називаються рівносильними (еквівалентними), якщо множини їх розв'язків (корінь) збігаються, тобто це такі рівняння, які мають ті самі корені. Рівносильними вважаються й рівняння, кожне з яких не має коренів.
Наприклад, рівняння х+1=7 і х+4=10 рівносильні, тому що кожне з них має єдиний корінь — число 6. Рівносильні й рівняння х2 = -4 і Зх2 +5 = 0 (на області дійсних чисел), тому що жодне з них не має коренів.
Рівняння х-8=1 і х2=81 не рівносильні, тому що рівняння х-8=1 має тільки один корінь х=9, тоді як рівняння х2 = 81 має два корені: х1 = 9 і х2 = -9.
Перетворення, при яких рівняння переходить у рівносильне йому рівняння
1) Якщо в рівнянні поміняти місцями ліву й правую частини, то вийде рівняння, рівносильне даному.
Наприклад, х + 4 = 2х + 9<=> 2х + 9 = х + 4.
2) Якщо в рівнянні який-небудь доданок перенести з одної частини в іншу, змінивши його знак на протилежний, то отримаємо рівняння, рівносильне даному.
Наприклад, 2х + 7 = х- 3<=>2 х-х = -7-3.
3) Якщо обидві частини рівняння помножити або розділити на одно й те ж відмінне від нуля число, то вийде рівняння, рівносильне даному.
Наприклад, рівняння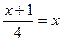 
рівносильне рівнянню х+1=4х (рівняння х+1=4х отримано з рівняння 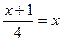множенням обох частин на число 4).
4) Якщо до обох частин рівняння додати або відняти одно и те ж число, то вийде рівняння, рівносильне даному.
Наприклад, х + 2 = 5х<=>х + 2 + 7 = 5х + 7; 5х + 2 = 0<=>5х + 2- 2 = 0- 2.
5) Якщо до обох частин рівняння додати або відняти будь-яку функцію, то вийде рівняння, рівносильне данному за умовою, що області визначення отриманого й данного рівняння збігаються.
Наприклад, х = 2<=>х + х2=2 + х2;
х3 + 5х = 8 + 5х <=> х3 = 8
