Тема 1. Основні види рівнянь з однією змінною.
І. Повторення і систематизація знань (читати)
Рівності та їх властивості. Тотожності.
Рівність — це два вирази, які з'єднані знаком «=».
х=у — це рівність, х — ліва частина рівності, у — права частина рівності.
Властивості рівностей:
1) х = у => у = х;
2) х = у, у = z => х = z;
3) х = у => х + z=у + z;
4) х = у => х z = у z;
5) х = у = > 
.
Рівність може бути числовою або зі змінними. Числова рівність може бути вірною або невірною.
Множина значень змінних, при яких ліва й права частини рівності мають сенс (визначені), називається областю визначення рівності й позначається звичайно через D
Тотожність — це рівність, яка вірна при будь-яких значеннях змінних з області визначення рівності.
Рівняння з однією змінною.
Рівнянням з однієї змінної називається рівність виду f(х) = φ(х), де f(х) і φ(х) — деякі задані функції. Величина х називається невідомою.
Усяке значення змінної х, при якому рівняння f(х) = φ(х) обертається у вірну числову рівність називається коренем або розв'язком рівняння. Розв'язати рівняння — це значить знайти всі його корені або довести, що їх немає.
Приклад 1. Рівняння х+2=5 має єдиний корень х=3, тому що при цьому й тільки при цьому значенні змінної рівняння х+2=5 обертається у вірну числову рівність 3+2=5. Якщо визначити S — множина коренів рівняння х+2=5, то S={3}.
Приклад 2. Рівняння (х+1)(х-3)(х-6)=0 має три корені:
х1 = -1, х2 =3, х3 = 6. S={-1; 3; 6} — множина коренів рівняння.
Відповідь: {-1; 3; 6}.
Приклад 3. Рівняння 2х+5=2 х-7 не має коренів, S=Ø.
Відповідь: Ø.
Приклад 4. Рівняння |х|= х має незліченна множина коренів (розв'язків), тому що будь-яке невід’ємне число х>0 є розв'язок цього рівняння. Звідси S = {х | х > 0}.
Відповідь: {х | х > 0}.
Приклад 5. Рівняння із двома змінними 2(х-у)=2 х-2у має незліченну множину розв'язків. Це рівняння є тотожністю і будь-які дійсні значення х та у є його розв'язком, S={(х;у) |х є R, у є R}.
Приклад 6. Рівняння х2=-16 не має дійсного корінь.
Відповідь: Ø.
Для того щоб знайти область визначення рівняння f(х) = φ(х) необхідно знайти перетин множин, на яких визначені задані функції f(х) і φ(х).
Приклад 7. Знайти область визначення рівняння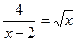 
Розв'язок. Маємо f(х) =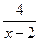 
, φ(х)= 
D1=(-∞;2) U (2; ∞); D2=[0; ∞).
Звідси D = D1∩D2=[0;2) U (2; ∞).
Відповідь: х є [0;2) U (2; ∞).
