Ірраціональними називають такі рівняння, у яких змінна знаходиться під знаком кореня. Наприклад, 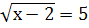 ,
,  .
.
!!! При розв’язуванні ірраціональних рівнянь обов’язковим є АБО знаходження ОДЗ рівняння, АБО перевірка знайдених коренів. Тому що при виконанні перетворень може порушуватись рівносильність рівнянь.
Основним методом розв’язування ірраціональних рівнянь є піднесення обох частин рівняння до одного степеня. На допомогу приходять формули скороченого множення  ;
; 
ПРИКЛАД 1.  . Оскільки
. Оскільки  , а -4
, а -4  0, то рівність неможлива.
0, то рівність неможлива.
Відповідь: коренів немає.
ПРИКЛАД 2.  .
.  ; х-1=8; х=9.
; х-1=8; х=9.
Відповідь: 9.
ПРИКЛАД 3. 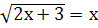 .
.  ; 2х+3=
; 2х+3=  ;
;  -2х-3= 0; х1=-1, х2=3.
-2х-3= 0; х1=-1, х2=3.
Перевірка. При х=-1 маємо  =-1 – неправильна рівність, отже, х=-1 - сторонній розв’язок. При х=3 маємо
=-1 – неправильна рівність, отже, х=-1 - сторонній розв’язок. При х=3 маємо 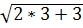 = 3 – правильна рівність, отже, х=3 – корінь.
= 3 – правильна рівність, отже, х=3 – корінь.
Відповідь: 3.
ПРИКЛАД 4.  +
+ 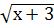 = 4. Ізолюємо один корінь і піднесемо обидві частини рівняння до квадрата.
= 4. Ізолюємо один корінь і піднесемо обидві частини рівняння до квадрата.  = 4-
= 4- 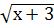 ;.
;.  =
=  ;
;
5х-1 = 16 - 8 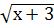 +
+  ; 5х-1 = 16 - 8
; 5х-1 = 16 - 8 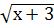 +х+3. Знову ізолюємо корінь і знову піднесемо обидві частини рівняння до квадрата. 8
+х+3. Знову ізолюємо корінь і знову піднесемо обидві частини рівняння до квадрата. 8 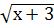 = 16 +х+3-5х+1;
= 16 +х+3-5х+1;
8 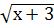 = 20 – 4х; 2
= 20 – 4х; 2 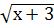 = 5-х;
= 5-х;  ; 4(х+3) = 25-10х+
; 4(х+3) = 25-10х+  ;
;
 -14х+13=0; х1=1, х2=13.
-14х+13=0; х1=1, х2=13.
Перевірка. х=1 – корінь; х= 13- сторонній розв’язок.
Відповідь: 1.
ПРИКЛАД 5. Розглянемо рівняння з кубічними коренями:  .
.
(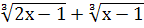 )3=13;
)3=13;
( )3+3(
)3+3( 2
2 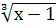 + 3
+ 3  )2+(
)2+(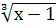 )3 = 1;
)3 = 1;
2х-1 + 3 
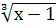 (
(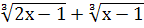 ) + х-1 = 1;
) + х-1 = 1;
3 
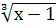 (
(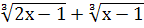 ) = 1-2х+1-х+1;
) = 1-2х+1-х+1;
3 
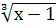 *1 = 3 – 3х;
*1 = 3 – 3х; 
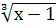 = 1 – х;
= 1 – х;
(
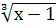 )3=(1 – х)3; (2х – 1)(х – 1) = (1 – х)3;
)3=(1 – х)3; (2х – 1)(х – 1) = (1 – х)3;
2х2 – 2х – х + 1 = 1 – 3х + 3х2 – х3; х3 – х2 = 0; х1=1, х2=0.
Перевірка. Заміна  порушує рівносильність, оскільки ця рівність виконується не при всіх значеннях х.
порушує рівносильність, оскільки ця рівність виконується не при всіх значеннях х.
х=1 – корінь; х= 0- сторонній розв’язок.
Відповідь: 1.
Ще один метод розв’язування ірраціональних рівнянь – заміна змінної.
Якщо до рівняння змінна входить в одному і тому самому вигляді, то зручно відповідний вираз позначити новою змінною.
ПРИКЛАД 6.  Нехай
Нехай  = t, тоді маємо
= t, тоді маємо 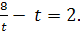 Звідки
Звідки
t1=-4, t2=2. Зробимо обернену заміну:  = -4 – коренів немає;
= -4 – коренів немає;  =2; х=2.
=2; х=2.
Відповідь: 2.
ПРИКЛАД 7.  =4. Запишемо рівняння у вигляді: 3(
=4. Запишемо рівняння у вигляді: 3( )2
)2  і зробимо заміну
і зробимо заміну  = t. Маємо:
= t. Маємо:  + t – 4 = 0; t1=1, t2 =
+ t – 4 = 0; t1=1, t2 =  .
.
Зробимо обернену заміну:  = 1; х = 0;
= 1; х = 0; 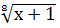 =
=  – коренів немає.
– коренів немає.
Відповідь: 0.
ПРИКЛАД 8.  Підкореневі вирази є взаємно оберненими, тому зробимо заміну
Підкореневі вирази є взаємно оберненими, тому зробимо заміну 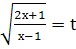 , тоді
, тоді  , отримаємо рівняння t -
, отримаємо рівняння t -  = 1, розв’язавши яке отримуємо: t1=-1, t2=2. Виконавши обернену заміну, маємо х=2,5.
= 1, розв’язавши яке отримуємо: t1=-1, t2=2. Виконавши обернену заміну, маємо х=2,5.
Відповідь: 2,5.
ПРИКЛАД 9. 2х2+6х -3  = 5. Запишемо 2(х2+3х) -3
= 5. Запишемо 2(х2+3х) -3  = 5.
= 5.
Заміна  = t, тоді
= t, тоді 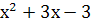 = t2, звідки
= t2, звідки  = t2
= t2 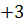 , і рівняння приймає вигляд 2(t2
, і рівняння приймає вигляд 2(t2 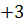 )-3t=5, звідки t1=1, t2=0,5.
)-3t=5, звідки t1=1, t2=0,5.
Зробимо обернену заміну:  = 1,; х1=1, х2= -4; х1=-1, х2=3.
= 1,; х1=1, х2= -4; х1=-1, х2=3.
 =
= 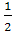 ; х1,2=
; х1,2=  .
.
Відповідь: 1;- 4;  .
.
Завдання:
1) Розібрати приклади 1-4.
2) Розв’язати № 616(1,3), 618(1,3,7), №623 (1)
3) Розібрати приклади 6-8.
4) Розв’язати №641(1,2,5,9)
5) Розібрати приклад 5.
6) Розв’язати  .
.
7) Розібрати приклад 9.
8) Розв’язати № 643(1,2)






