Рассматриваем поля, которые зависят от времени по закону:
И рассмотрим уравнения Максвелла:
Если учитывать временную зависимость для Е и Н и если ввести 
, то получим:
Теорема взаимности рассматривает две группы источников и полей. Источником является ток 
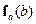- поле 
, создаваемое источником «а» в области «b». Таким образом, источник 
порождает поля 
и 
, а 
порождает поля 
и 
.
Перепишем уравнения Максвелла для 1 и для 2 источников:
и 
и 
Для первого источника, умножим левое и правое уравнение скалярно на и соответственно, и к первому прибавим второе:
(*)
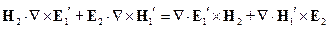
Для второго источника:
(**)
Из (*) вычтем (**):
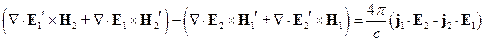
Проинтегрировав обе части этого уравнения по объему и, используя теорему Остроградского-Гаусса, получим:
Здесь предполагается, что поле на бесконечности обращается в нуль, это обращение происходит за счет поглощения волны, тогда:
и значит:
- теорема взаимности для излучения
Этот интеграл берется по областям, где есть источники. Области источников ограничивают области интегрирования. Там, где нет источников, этот интеграл равен нулю.
То есть перемена местами источников и полей не меняет результата.
Предполагая, что поле достаточно медленно меняется в достаточно малой области локализации источников, можно поле вынести за знак интеграла, тогда:
Тогда:
- теорема взаимности для дипольного излучения.
Используем приближение линейного тока:
Если контуры замкнутые, то 
- падение напряжения на 1-м контуре за счет излучения 2-го источника. Обозначим 
и 
, тогда:
Мы получили теорему взаимности для контуров, реагирующих на излучение.
Задачи по курсу «Электродинамика сплошных сред»
| 1. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r. |
2. Вычислить    где p – постоянный вектор.
|
3. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:
если объем, который охватывает замкнутая поверхность, равен V; A – постоянный вектор.
|
4. В равномерно заряженном шаре с объемной плотностью заряда  имеется шарообразная полость, центр которой расположен на расстоянии  от центра шара. Найти напряженность электрического поля внутри полости, внутри шара и снаружи шара. Радиусы шара и полости равны соответственно R и  .
|
| 5. Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара. Объемная плотность заряда равна , радиус шара R.
|
| 6. Определить коэффициенты разложения потенциала точечного заряда в интеграл Фурье. |
7. Найти потенциал, создаваемый зарядом, распределенным в бесконечной среде по закону: 
|
8. Определить потенциал точечного заряда  , находящегося в однородной анизотропной среде с заданным тензором диэлектрической проницаемости  .
|
9. Найти напряженность магнитного поля внутри цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностью  . Оси цилиндра, образующего полость, и цилиндрического проводника параллельны и находятся друг от друга на расстоянии .
|
10. Показать, что постоянное однородное магнитное поле B можно описывать векторным потенциалом А=  .
|
| 11. Найти интенсивность излучения частицы массы m, движущейся по круговой орбите радиуса , под действием кулоновских сил. Выразить ответ через энергию частицы.
|
| 12. Определить напряженность и потенциал электростатического поля равномерно заряженного шара радиуса R. Суммарный заряд шара Q. |
| 13. Вычислить энергию электростатического поля равномерно заряженного шара радиуса R. Суммарный заряд шара Q. |
14. Средняя плотность заряда электронного облака в атоме водорода описывается функцией  , где a – боровский радиус, а r – расстояние до протона, имеющего заряд e. Чему равна электростатическая энергия взаимодействия протона с электронным облаком.
|
| 15. Вычислить дипольный момент равномерно заряженного полушара радиуса R, суммарный заряд полушара Q. Отрицательный заряд – Q, помещен на расстояние l от центра по оси симметрии. |
| 16. Определить дипольный и квадрупольный моменты системы, сдвинутой от начала координат на вектор c. |
17. Внутри шара радиуса задан вектор плотности тока  . Найти распределение векторного потенциала внутри и снаружи шара.
|
18. Заряд e совершает гармонические колебания вдоль оси X по закону  . Написать выражение для объемной плотности  заряда и объемной плотности  тока. Найти средние по времени за период  объемные плотности заряда  и  .
|
19. Радиус-вектор  точки расположения диполя с моментом  меняется во времени по закону  . Определить распределение объемных плотностей заряда и тока в пространстве. Вычислить магнитный момент  найденного тока
|
20. Простейшая линейная антенна представляет собой тонкий прямолинейный провод длины l, по которому течет ток  . Определить интенсивность I длинноволнового излучения антенный в среднем за период колебания тока.
|
21. Протон с массой m и зарядом e движется перпендикулярно однородному постоянному магнитному полю с напряженностью  . Его кинетическая энергия в начальный момент времени  равнялась  . Найти закон убывания кинетической энергии  , обусловленный дипольным излучением.
|
22. В классической модели атома, предложенной Резерфордом, электрон с зарядом e и массой m вращается по круговой орбите вокруг неподвижного ядра с зарядом Z|e|. Найти закон убывания полной энергии электрона, обусловленный дипольным излучением. Вычислить время  , по истечении которого, электрон упадет на ядро вследствие потери энергии на дипольное излучение. В начальный момент времени электрон находился на расстоянии R от ядра.
|
| 23. Доказать, что у замкнутой системы заряженных частиц с одинаковым отношением заряда к массе дипольное излучение отсутствует. |
| 24. Простейшая рамочная антенна представляет собой прямоугольную рамку со сторонами a и b, по которым течет линейный ток . Определить интенсивность I длинноволнового излучения антенны в среднем времени за период колебаний тока.
|
| 25. При каком условии интенсивность магнитно-дипольного излучения не зависит от выбора начала координат? |
| 26. При каком условии интенсивность квадрупольного излучения не зависит от выбора начала координат? |
