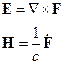¬ этом случае надо учитывать оба слагаемых в скал€рном потенциале.
ѕотенциалы:

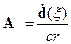
’арактерный размер 
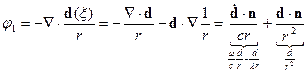
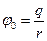 ,
, 
“огда имеем:
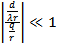 (*) и
(*) и  (**)
(**)
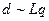
»з (*) 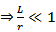 , а из (**)
, а из (**) 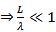 . » мы приходим к условию
. » мы приходим к условию  . «десь три варианта св€зи
. «десь три варианта св€зи 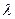 и
и 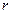 :
:
¬олнова€ зона:
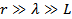

1) Ѕлижн€€ зона:

2) »ногда под ближней зоной понимают:
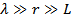
«десь везде  определ€ет дипольное излучение.
определ€ет дипольное излучение.
ћы рассматриваем случай  , тогда в потенциале
, тогда в потенциале  имеетс€ два слагаемых одного пор€дка и их оба надо учитывать. «аметим, что
имеетс€ два слагаемых одного пор€дка и их оба надо учитывать. «аметим, что 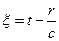 , тогда:
, тогда:
 - сферически симметричное решение волнового уравнени€
- сферически симметричное решение волнового уравнени€
¬олновое уравнение:
ð 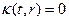
Ёта функци€ Ц сферически симметрична€, т.е. она зависит от модул€ вектора 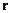 , тогда решение волнового уравнени€ по сфере одного радиуса одинаковые.
, тогда решение волнового уравнени€ по сфере одного радиуса одинаковые.
ð 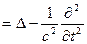
ќператор Ћапласа в сферических координатах имеет вид:
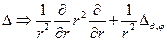 , где
, где 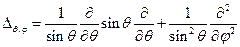
Ќо  , тогда:
, тогда:
ð 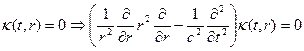
»ли
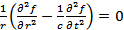 , где
, где 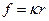
–ешение этого уравнени€ аналогично случаю плоских волн, тогда:

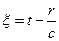 - дл€ расход€щейс€ волны.
- дл€ расход€щейс€ волны.
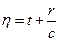 - дл€ сход€щейс€ волны.
- дл€ сход€щейс€ волны.
‘ронт волны 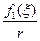 - расход€ща€с€ сфера. ћы показали, что
- расход€ща€с€ сфера. ћы показали, что  - это сферически симметрична€ функци€.
- это сферически симметрична€ функци€.
ð 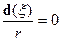

»спользуем это выражение дл€ нахождени€ полей:

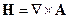
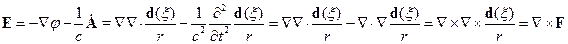

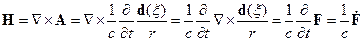
“аким образом, мы получили: