Запишем уравнения Максвелла:
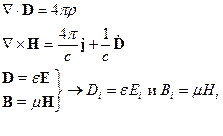
Здесь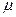 
и 
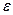- числа, а векторы 
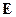и 
, 
и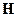 
коллинеарные.
Для однородных изотропных сред имеем:
Используем Калибровку Лоренца
ð 
ð 
Мы получили уравнение Даламбера для скалярного потенциала электромагнитного поля в случае однородной изотропной среды.
ð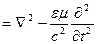 
Запишем 4-ое уравнение Максвелла в среде без учёта пространственной дисперсии:
из (1) и (2) следует:
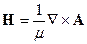
из (3) и (4) следует:
Используем то, что среда однородна и изотропна и запишем 4-е уравнение Максвелла:
Сгруппируем элементы, подчёркнутые двумя линиями:
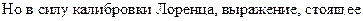в скобках, даёт нуль.
Теперь сгруппируем элементы, подчёркнутые одной линией. В результате получаем:
ð 
ð 
В итоге мы получили уравнение Даламбера для векторного потенциала электромагнитного поля в случае однородной изотропной среды.
