Перейдём к тензорам второго ранга 
. Получим:
(
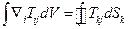
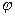- скалярная функция), тогда:
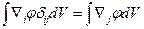
В результате получаем:
- более общая модификация теоремы Остроградского-Гаусса.
Потенциалы электромагнитного поля в вакууме.
Удобно ввести:
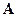-векторный потенциал
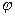-скалярный потенциал
однозначно определяют электромагнитное поле
Градиентная инвариантность.
Существует преобразование, которое не меняет полевых характеристик 
. Таким преобразованием является градиентное:
Здесь 
– произвольная функция координат и времени 
-инвариантность полевых характеристик
относительно градиентных преобразований.
Аналогично для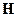 
:
На потенциалы 
могут быть наложены произвольные, удобные для исследования ограничения – калибровки потенциалов, т.к. - произвольная.
