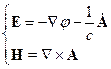
Перепишем уравнения Максвелла:
|
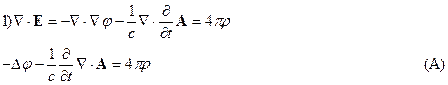
1.Калибровка Лоренца
Тогда уравнение (А) перепишется в следующем виде:
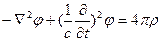
ð 
ð 
- уравнение Даламбера
Это уравнение есть – неоднородное дифференциальное уравнение в частных производных.
ð - оператор гиперболического типа.
Для уравнения (В) имеем:
ð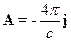 
Все, имеющие физический смысл, результаты должны быть градиентно-инвариантными:
В силу калибровки Лоренца получаем:
ð 
Т.е. функция 
должна удовлетворять однородному уравнению Даламбера (его ещё называют волновым уравнением)
2.Калибровка Кулона
- калибровка Кулона
Уравнение (А) перепишется в следующем виде:
- уравнение Пуассона.
Если же 
(в пустоте), то уравнение Пуассона принимает вид:
-уравнение Лапласа.
получаем, что функция должна удовлетворять уравнению:
3.Калибровка поперечных волн
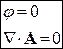
Полагаем 
есть функция только координат.
Значит функция должна удовлетворять уравнению:
