Электроакустические сигналы

Для начала нужно ввести некоторые определения, наибо­лее часто встречающиеся в специальной литературе. В пер­вую очередь к таковым относится понятие сигнала.

Сигналом мы называем любую информацию, независимо от её физического вида: акустический (механический) сиг­нал — движение частиц воздушной или жидкой среды, несу­щее звук от источника к слушателю; электрический сигнал — сообщение, передающееся по проводникам в форме электри­ческого тока; магнитный сигнал — информация, зафиксиро­ванная на ленте магнитофона в виде так называемой оста­точной намагниченности; оптический сигнал, передающий изображение, и т. д. Надо сказать, что информация, произво­дящая психофизические впечатления, в математической форме является величиной переменной. Действительно, по­стоянное атмосферное давление не вызывает слуховых ощу­щений, так же, как не вызывает зрительных ощущений пол­ный постоянный мрак.

Простейшим информационным сигналом, знакомым каж­дому со школьной скамьи, является синусоидальное (цикли­ческое, периодическое) колебание, характеризуемое частотой (или периодом), амплитудой и относительной фазой, когда идёт речь о временном сопоставлении двух сигналов (рис. 2-1).

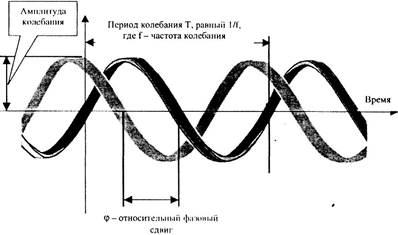
Рис. 2-1

№ Х20

Механическим видом такого сигнала считаются, напри­мер, колебание маятника, фрагмент колебания камертона (именно фрагмент, потому что все, возбуждённые ударом, колебания камертона будут постепенно затухать, т. е. их ам­плитуда плавно уменьшится до нуля). В такой же математи­ческой форме представляется простейший акустический сиг­нал, чистый тон — звучание того же камертона.

Практически, все остальные сигналы, несущие какую-либо информацию, уже не описываются простейшими фор­мами, а представлены спектром (рис. 2-2), в набор которого входит конечное или бесконечное число синусоидальных ко­лебаний, суммированных при определённом соотношении их амплитуд, частот и фаз, а то и вовсе сложенных хаотично. Пример последнему — акустический шум.

Собственно амплитуда, как и вообще так называемое мгновенное значение простейшего колебания представляет интерес только для математиков и создателей технических устройств. В нашей практике актуальны энергетические, мощностные характеристики сигналов, косвенным прибли­зительным отражением которых является их индикация на шкале измерителей уровней при звукозаписи или передаче. Под уровнем понимается величина сигнала, соотнесённая с каким-либо эталоном. Так, если сигнал сложного спектра по своей суммарной, интегральной мощности равен эталонно­му, его уровень считается 100-процентным. Половина мощ­ности соответствует 50 %, треть ~ 33 %, и т. д.

Надо сказать, что используемые в нашей практике изме­рители уровня сигналов интегрируют их мощность в тече­ние очень малого времени, от сотен микросекунд до единиц миллисекунд, чтобы звукорежиссёр мог следить за текущей динамикой, так что видимый диапазон индикаций адеква­тен динамическому диапазону звукопередачи лишь с опре­делёнными приближениями. Чем меньше время интегриро­вания, тем безынерционнее, точнее происходит измерение, что, впрочем, имеет скорее технический смысл, нежели от­ражает динамические свойства звука. Действительно, слы­ша crescendo в оркестровом tuttu вряд ли мы, в отличие от безынерционного измерителя, станем одновременно реаги­ровать на vibrato флейт как на колебания суммарной громко­сти. Тем не менее, как будет показано ниже, точность инди­кации уровня звукопередачи важна для гарантии качества фонограммы.

Рис. 2-2

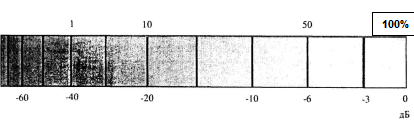
Учёт уровней звуковых сигналов в линейных процентных величинах не соответствует той шкале ощущений, что свой­ственна нашему слуху. Мы оцениваем изменения громкости в логарифмическом масштабе, и это позволяет нам воспри­нимать огромный, в арифметическом смысле, динамический диапазон звуков — с более чем миллионным перепадом. По-этому в электроакустике принята шкала отсчёта уровней, аналогичная слуховой: в относительных логарифмических единицах — децибелах (дБ). Ступенька такой шкалы в элект­роакустических измерениях составляет 20 lg A1/A2, где А1 и А2 — сопоставляемые величины, одна из которых, в боль-шинстве случаев А2, может являться эталонной, или, как выражаются инженеры, опорной. Поскольку в современной звукозаписывающей технике часто за опорный сигнал при­нимается максимально допустимый, то уровень текущего сиг­нала А1 в сравнении с ним может варьироваться в диапазо-неот О дБ до каких-либо отрицательных значений. Так, с из-вестным округлением, половина максимального уровня в логарифмическом масштабе равна величине в минус 6 дБ, треть — минус 10 дБ, четверть — минус 12 дБ, десятая часть — минус 20 дБ и т. д. Соответственно, увеличение уровня сигнала

 

по сравнению с его предыдущим значением отмечается, как прирост на то или иное количество «положительных» деци­бел (рис. 2-3).

 

Рис. 2-3

Измерители текущего уровня реальных сигналов, как пра­вило, не реагируют на короткие всплески последних, так на­зываемые пики, и предоставленные звукорежиссёру индика­торы показывают усреднённые значения уровней. Между тем, величина пиковых значений бывает очень существенна; для их практической оценки следует помнить о таком параметре натуральных акустических сигналов, как пик-фактор. Он отражает степень превышения пиковых значений сигналов того или иного рода над его средними значениями.

Величина пик-фактора может превышать 20 дБ.

Период колебаний является величиной производной; тра­диционно оперируют обратным понятием — частотой, изме­ряемой в герцах (ГЦ). Для музыкального слуха, на первых по­рах, частоту акустических сигналов можно ассоциировать с высотой звуков, если, конечно, говорить об основных тонах звучаний, без учёта обертонов, гармоник натурального ряда, хорошо известных людям, получившим музыкальное обра­зование. И хотя психоакустики доказали отсутствие абсолют­ных интервальных соотношений частот и высот звуков вдоль всей темперированной шкалы, на практике можно полагать, что октавное повышение адекватно удвоению частоты сиг­нала, а октавное понижение — её делению пополам. В осо­бенности это справедливо для звуков среднего регистра, от малой до третьей октавы. Для оценки частоты звукового сиг­нала музыканты пользуются точкой отсчёта в 440 герц, что соответствует камертонному ля первой октавы.

К слову, способность человеческого слуха отмечать рав­ными относительные интервалы звуков, независимо от

регистра, лишний раз доказывает логарифмическую приро­ду нашего восприятия. И здесь, как при оценке динамичес­ких диапазонов, вся область рационально слышимых частот из 18-20 тысяч герц превращается в какой-нибудь десяток октав.

В главе «ФОНОКОЛОРИСТИКА» читатель получит под­робные сведения о спектрах сигналов и о практическом от­ношении к частотам и частотным диапазонам.

О фазовых характеристиках сигналов в нашей практике можно говорить, рассматривая, по меньшей мере, их пару. Фаза — понятие временное, показывающее, насколько один сигнал отстаёт от другого или опережает его, но такая оцен­ка актуальна только при сравнении тональных сигналов с равными частотами, или двух одинаковых по частоте спек­тральных компонент сложных сигналов.

Рис. 2-4

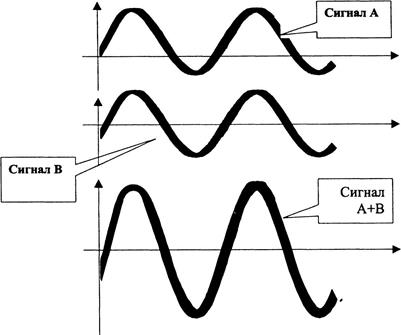
На рисунках 2-4 и 2-5 даны в тригонометрическом пред­ставлении пары одинаковых сигналов А и В. В первом случае

 

эти два сигнала являются синфазными — увеличение и умень­шение мгновенных значений во времени совпадает. При их сложениии итоговый сигнал А+В оказывается вдвое большим каждого из исходных. Несложно убедиться в том, что взаим­ное фазовое смещение любого из сигналов смешиваемой пары приведёт к заметному уменьшению их суммы (рис. 2-5).

В школьном курсе физики рассматривалось явление ин­терференции колебаний и волн, подробно поясняющее наши примеры.

ческих нарушений или неудачной установки микрофонов, она сказывается на чёткости стереофонического изображения (смотри главу «ФОНОГРАФИЧЕСКАЯ КОМПОЗИЦИЯ»),

вплоть до полной её неопределённости, а при монофоничес­ком воспроизведении стереозаписи, когда суммируются сиг­налы левого и правого стереоканалов, противофаза, благо­даря интерференции, может привести если не к полному пропаданию звука, то, по меньшей мере, к сильному нару­шению громкостных или тембровых качеств.

 

Рис. 2-5

Экстремальным случаем в звукорежиссёрской практике считается взаимный фазовый сдвиг изоморфных сигналов на 180°, так называемая «противофаза». Вследствие техни-

Рис. 2-6

Практический контроль фазовых соотношений осуществ­ляется с помощью так называемых кореллометров или гони­ометров, отражающих тенденцию преимущественного со­впадения или антисовпадения фаз спектральных компонент двух сложных сигналов.

На рисунке 2-6 приведены две гониограммы двухканаль-ного стереофонического сигнала, левая из которых, согласно международному стандарту, принятому для грамзаписи, ил­люстрирует преимущественную противофазность, а пра­вая — преимущественную синфазность стереопары. Сказан­ное отображается вертикальной или горизонтальной ориентацией гониограмм, соответственно тенденциям фазо­вых взаимоотношений.

 

38

Величина сигнала

Электронные устройства могут генерировать синусои­дальные колебания заданной амплитуды и частоты или иные колебания различного рода (в том числе и шум); их вид адекватно изображается на экране специального при­бора— осциллографа, с помощью которого технические со­трудники студий исследуют интересующие их параметры сигналов.

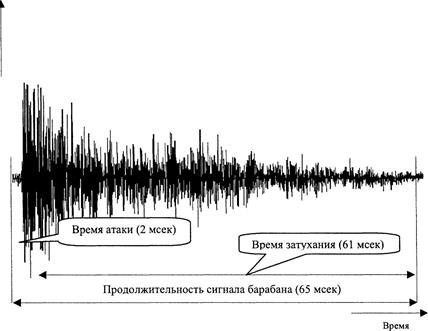
К характеристикам сложных реальных сигналов, с кото­рыми постоянно имеют дело звукорежиссёры, следует отнес­ти так называемую огибающую амплитуд, иллюстрирующую сигнал в его динамическом развитии (рис. 2-7).

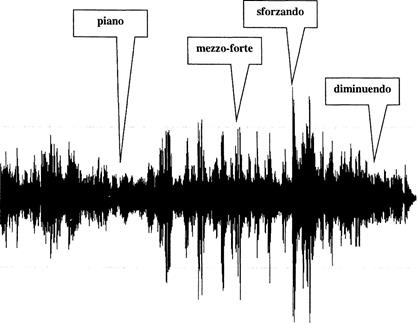
Рис. 2-7

Информация, которую можно черпать из рисунка огиба­ющей, увеличенного до деталей, позволяет судить о характе­ре и времени атаки (нарастания) и затухания звуков; эти дан­ные бывают актуальны при использовании приборов для динамической обработки сигналов (рис. 2-8).

Рис. 2-8