При рассмотрении установившегося движения самолетов с турбореактивными двигателями для определения летно-технических характеристик самолета удобно пользоваться методом тяг, который разработал Н.Е. Жуковский. Метод тяг Жуковского основан на сравнении величин потребной и располагаемой тяг.
Потребной тягой P п называется тяга, необходимая для установившегося горизонтального полета на данной высоте с заданной скоростью. Она численно равна силе лобового сопротивления самолета:
. (63)
Располагаемая тяга P р– это максимально возможная суммарная тяга всех двигателей самолета на данной высоте и при данной скорости полета.
Сравнение потребной и располагаемой тяг удобно осуществлять, построив совмещенный график зависимостей Р п и Р р от скорости полета V для данной высоты полета и данной массы самолета (см. рис. 42). Такой график называется диаграммой потребных и располагаемых тяг. Рассмотрим характерные точки на этой диаграмме.
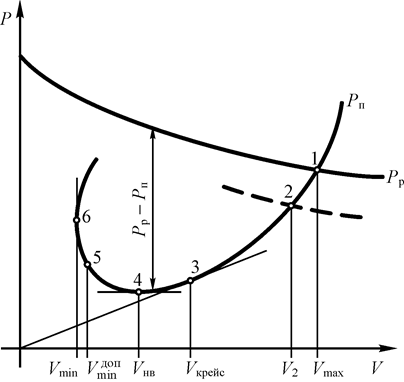
Рис. 42. Диаграмма потребных и располагаемых тяг
Точка «1», где пересекаются кривые потребных и располагаемых тяг, очевидно соответствует режиму максимально возможной скорости установившегося горизонтального полета V max, т.к. при большей скорости полета потребная тяга будет превышать располагаемую. Точки же, лежащие на кривой Р п = f (V) левее точки «1» (например, точка «2»), соответствуют установившемуся горизонтальному полету со скоростью, меньшей V max, в данном случае – со скоростью V 2. Для осуществления такого режима полета необходимо несколько уменьшить тягу двигателя (см. кривую, выполненную штриховой линией) и увеличить коэффициент подъемной силы Cya. Не вдаваясь в подробности отметим, что летчик имеет возможность в полете управлять тягой двигателя и подбирать угол атаки, обеспечивающий требуемый Cya.
Характерной точкой, представляющей особый интерес, является точка «3», которая является точкой касания прямой, проведенной из начала координат к кривой потребных тяг Р п = f (V). Очевидно, что в данной точке отношение 
будет минимальным. При выполнении этого условия, как это станет ясно в дальнейшем, обеспечивается максимальная дальность полета.
В точке «4» потребная тяга Р п минимальна. Перепишем формулу (47) для условий установившегося горизонтального полета:
. (64)
Если Р п – минимальна, то аэродинамическое качество K будет максимальным. В разделе, посвященном аэродинамическому качеству (см. п. 1.6.6), мы отметили, что коэффициент подъемной силы и угол атаки, соответствующие максимальному значению качества называются наивыгоднейшими. Отсюда и скорость, соответствующая минимальному значению потребной тяги, также называется наивыгоднейшей и может быть вычислена по формуле:
. (65)
При дальнейшем уменьшении скорости для обеспечения установившегося горизонтального полета наряду с увеличением угла атаки необходимо увеличивать тягу двигателей, т.к. здесь начинает быстро расти индуктивное сопротивление, что приводит к общему увеличению потребной тяги.
Точка «6» соответствует минимальному значению скорости установившегося горизонтального полета V min. При этом значении скорости необходимо, чтобы самолет летел с максимальным значением коэффициента подъемной силы Cya max, т.е. на критическом угле атаки aкр. По соображениям безопасности полет на критическом угле атаки считается недопустимым, т.к. любая ошибка в пилотировании или вертикальный порыв ветра, приводящие к дальнейшему увеличению угла атаки, вызовут резкое уменьшение Cya из-за отрыва потока на крыле, что приведет к сваливанию самолета. Поэтому на практике за минимально допустимую скорость полета 
принимают скорость, несколько большую, чем V min (см. точку «5»). Коэффициент подъемной силы при этом берут несколько меньшим: Cya доп» 0,8…0,85 Cya max. Минимально допустимая скорость полета вычисляется по формуле:
. (66)
С помощью диаграммы потребных и располагаемых тяг можно легко определить максимальную скороподъемность Vy max на данной высоте и соответствующую ей скорость набора высоты V наб.
Из уравнений движения при наборе высоты (52) вытекает, что:
, (67)
или, что то же самое:
. (68)
Перепишем формулу для скороподъемности (53) с учетом (68):
. (69)
Из формулы (69) видно, что скороподъемность зависит от избытка тяги (Р р – Р п). Очевидно, что максимальная скороподъемность будет при максимальном избытке тяги, т.е. когда разность (Р р – Р п) максимальна. Найти эту максимальную разность и соответствующую ей скорость набора высоты V наб можно графически (см. рис. 42), а затем по формуле (69) рассчитать максимальную скороподъемность Vy max на данной высоте.
С увеличением высоты полета располагаемая тяга падает, а минимальные значения потребной тяги не изменяются (см. рис. 43).
Рис. 43. Изменение потребной и располагаемой тяг в зависимости от
высоты полета
Наступает такой момент, когда кривые потребных и располагаемых тяг имеют только одну точку пересечения (при этом Vy max = 0). На этой высоте установившийся набор высоты невозможен, а установившийся горизонтальный полет возможен только на скорости V т. Такая высота называется теоретическим потолком самолета. Однако достичь теоретического потолка самолет в установившемся наборе высоты практически не может, т.к. время набора высоты при этих условиях стремится к бесконечности. Поэтому вводится понятие практического потолка – высоты полета, при которой максимальная скороподъемность не меньше заданной. Для дозвуковых самолетов Vy max ³ 3…5 м/с.
