, (2.4)
где s(t) – сигнал на одном периоде повторения. Ниже представлены соответствующий М-файл и график периодического сигнала (рисунок 2.4).
| function s=cosinobn1(t,Um,T,Uo) % s=cosinobn1(t,Um,T,Uo) % t - вектор текущего времени % Um - амплитуда % T - период косинусоиды % Uo - уровень отсечки | T2=T/2; % Приведение к периоду около нулЯ dt=abs(mod(t+T2,T)-T2); % Обращение к функции вычислениЯ % на одном периоле s=cosinob1(dt,Um,T,Uo); |
Рисунок 1.4 - Исследуемый сигнал на нескольких периодах повторения
2.3.3 Амплитудный и фазовый спектры периодического сигнала
Определим коэффициенты ряда Фурье периодического сигнала. Поскольку сигнал симметричен относительно начала отсчета времени, то коэффициенты ряда 
в формуле (1.5) будут равны нулю:
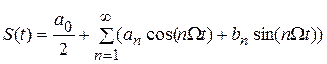, (1.5)
а ненулевые коэффициенты 
определяются по формуле
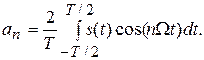(1.6)
Приведём аналитические выражения и сделаем расчет коэффициентов в формуле (1.6) (коэффициенты Берга) с помощью системы MATLAB.
function B=BergN(n,Um,Uo,O)
% Расчёт коэффициентов Берга
% B=BergN(n,O,Um,Uo)
% n – номер коэффициента Берга
% O – угол отсечки
% Um – амплитуда косинусоиды
% Uo – уровень отсечки
% B0(O)=(sin(O)-h*cos(O))/pi
% B1(h)=(O-sin(O)*cos(O))/pi
% Bn(h)=2*(sin(n*O)*cos(O)-n*sin(O)*cos(n*O))/(pi*n*(n*n-1))
if nargin == 3
O = acos(Uo/Um);
end
k=length(n);
B=zeros(1,k);
for i=1:k
switch n(i)
case 0, B(i)=Um*(sin(O)-O*cos(O))/pi;
case 1, B(i)=Um*(O-sin(O)*cos(O))/pi;
otherwise
m=n(i);
B(i)=2*Um*(sin(m*O)*cos(O)-...
m*sin(O)*cos(m*O))/(pi*m*(m*m-1));
end
end
Задав в командной строке системы MATLAB команду
n = 0:10; a = BergN(n,2,1);
получим набор коэффициентов , n = 0…10:
0.2180 0.3910 0.2757 0.1378 0.0276 -0.0276 -0.0315 -0.0098 0.0098 0.0138 0.0050.
Построим амплитудную спектральную диаграмму периодического сигнала (рисунок 1.5), используя команду stem(n,a*T). Амплитуды спектра представлены в илливольтах. Фазовая диаграмма у этого сигнала тождественно равна нулю вследствие его четности.
Рисунок 1.5 - Диаграмма амплитудного спектра периодического сигнала
