В предыдущем пункте было показано, как представлять сигнал одним выражением (одной функцией). Довольно часто имеется упорядоченный набор функций 
, и сигнал представляется взвешенной суммой функций этого набора 
. Например, если сигнал определён как взвешенная сумма пяти слагаемых (сумма произвольных функций, умноженных на фиксированные числа) 
, то для любого момента времени можно вычислить его значение по следующей последовательности команд:
1. Задание вектора коэффициентов (числовой массив) и вектора функций (массив ячеек):
c = [-5 4 -3 2 -1];
Sn = {'t' 't.^2’ 'sin(t)' 'cos(t)' 'exp(t)'};
2. Задание моментов времени вычисления значений сигнала:
t=0:0.1:0.4;
3. Использование цикла по пяти функциям с последующим суммированием:
for i =1:5
s(i,:) = c(i)*eval(char(Sn(:,i)));
end
x=sum(s(1:5,:))
4. Результат вычислений:
x= 1.0000 0.1253 -0.6973 -1.4657 -2.1780
В радиотехнике часто используется представление детерминированных сигналов в виде рядов по системам функций, например, полные ортонормальные системы для замкнутого интервала e = [-1, 1]. Такой интервал удобен для последующего перехода к любому другому интервалу путём подходящего масштабирования.
Наиболее известным и применяемым является ряд Фурье 
, в котором использованы комплексные гармонические функции 
, ортонормальные с весом 
, причём коэффициенты ряда вычисляются по известной формуле: 
. Количество членов n ряда Фурье при моделировании всегда ограничено, поэтому всегда имеется некоторая, но контролируемая погрешность представления функции таким рядом. Поскольку ряд Фурье является элементом гильбертового пространства, то ошибка аппроксимации представляет собой монотонно убывающую функцию от N – числа учитываемых членов ряда. Её величина полностью зависит от поведения моделируемой функции, точнее, от скорости её изменения. Поэтому часто на моделируемую функцию накладываются ограничения, например она не должна иметь на интервале [-1, 1] конечные разрывы. Несоблюдение этого условия приводит к так называемому явлению Гиббса, когда моделируемая функция колеблется около точки разрыва вокруг истинного значения.
Пример представления разрывной функции 
показан на рисунке 1.1. За счёт ограниченности ряда ошибка имеет величину порядка 4 % при n =10, 0.4 % при n =100 и т.п. На рисунке справа отчётливо видно, что абсолютное отклонение моделируемого процесса от истинного значения с увеличением n не уменьшается, имея значение около 18 % от величины разрыва.
| 
|
Рисунок 1.1 – Поведение суммы гармоник около точки разрыва (явление Гиббса)
| n = 50; % Число членов рЯда m = 500; % Число врем.отсчётов t = linspace(-1,1,m); V = ones(2*n+1,m); for k = -n: n V(k+n+1,:)=k*V(k+n+1,:); end for I = 1: m V(:,i)=t(i)*V(:,i); end E = exp(j*pi*V)'; c = symmst(-n: n)'; x = real(E*c)/sqrt(2); % x(t) | function c=symmst(n) %c(k)- коэффициенты Фурье ln = length(n); for i = 1: ln k = round(n(i)); c(i)= j*sqrt(2)*sin(pi*k/2)*... sinc(pi*k/2); end function s = sinc(x) if abs(x) < = 1e-12 s = 1; else s = sin(x)/x; end |
Другой часто используемой системой базисных функций для представления непрерывных сигналов являются полиномы Чебышева 1-го рода. При нормировочной функции 
полиномы 
образуют ортонормальную систему. Они вычисляется либо прямо по формуле 
, 
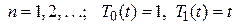, либо по рекуррентной формуле 
при тех же начальных условиях. Из всех полиномов, имеющих коэффициент, равный 1 при 
, полином 
наименее отклоняется от нуля в интервала [-1,1]. Вне интервала [-1,1] полином очень быстро возрастает (рисунок 1.2, а).
| 
| |
| Рисунок 1.2 – Функции Чёбышева вне интервала (-1,1) – а; на интервале (0,1) – б | ||
| t = 0:0.001:1.5; for n = 1: 10 y(n,:) = tcheb(n, t); end plot(t, y') % ФункциЯ пользователЯ function y = tcheb(n, t) % y = tcheb(n,t) % Вычисление полинома Чебышева T0 = ones(1,length(t)); T1 = t; | if n = = 0 y=T0; elseif n = = 1 y = T1; else for i =2: n T2 =2* t.*T1-T0; T0 = T1; T1 = T2; end y = T2; end | |
Один из самых простых базисов на интервале [0,1] – это мультипликативно-ортогональный базис, состоящий из одинаковых величине и по длительности импульсов, сдвинутых относительно друга на их ширину (рисунок 1.3) 
. Название связано с тем, что простое умножение двух функций из этого базиса является их скалярным произведением: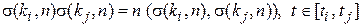 
.
| Рисунок 1.3 – Мультипликативный базис при n = 8 | ||
| function f = mob(k, n, t) % f = mob(k, n, t) t1 = rem(t,1); m = length(t1); f = zeros(1,m); if k = = 0 return end if k > n error(['k>n->[k n]=['num2str(... [k n]) ']']) | else g1 = (k-1)/n; g2 = k/n; for i = 1:m if t1(i) >= g1 & t1(i) <= g2 f(i) = 1; end end end | |
Функции Уолша также ортогональны на конечном интервале [-1/2, 1/2]: 
Символ [ n /2] означает наибольшее целое, меньшее или равное n /2, число p может принимать значения 0 или 1. Функция нулевого порядка 
Другой вариант функций Уолша, ортогональный на [0, 1], представлен на рисунке 1.4. В этом случае процедура вычисления 
достаточно проста:
- число k представляется в двоичном коде 
;
- вычисляются функции Радемахера 
;
- определяется степень 
, где 
– операция «исключающее или», при этом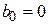 
;
- функция 
.
Рисунок 1.4 – Функции Уолша порядка 0.. 8
| function w = wal(k,t) % w = wal(k,t) t1 = rem(t,1); t1(1)=t1(1)+3*eps; t1(end)=t1(end)-3*eps; w = ones(1,length(t1)); if k == 0 w = w; return end b = [dec2binvec(k) 0]; n = length(b); for i = 1: n-1 r = xor(b(i),b(i+1)); if r ~= 0 w=w.*Rdm(i, t1); end end function r = Rdm(i,t) r = sign(sin(2^I*pi*t)); |
На полубесконечном интервале 
полиномы Лаггера 
; 
образуют также ортонормальную систему с весом 
: 
. Эти функции имеют важное значение для практики, поскольку импульсные реакции многих электрических цепей и систем представляются взвешенными суммами 
.
| 
|
| Рисунок 1.5 – Полиномы Лаггера n =1.. 10 – а; весовые функции – б | |
| function L = Lagger(n, t, w) L = Lagger(n, t, w) % Вычисление полинома Лаггера L0 = ones(1,length(t)); L1 = 1-t; if n = = 0 L = L0; elseif n = = 1 L = L1; else for i = 2:n L2=(2*i-1-t).*L1-(i-1)^2*L0; L0 = L1; L1 = L2; end L = L2; end | % Вычисление весовых функций % по признаку ‘w’ if nargin = = 3 & w = = 'w' x = exp(-t/2); if n = = 0 | n = = 1 L = L.*x; else for i = 2: n x = x/i; L = L.*x; end end end |
