Она определяется по формуле прямого преобразования Фурье
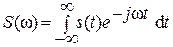, (1.8)
от сигнала (1.1), имеющего ненулевые значения на интервале (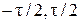
):
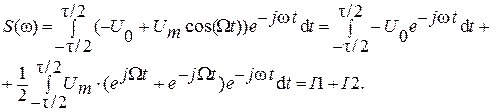
Первый интеграл равен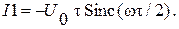 
Второй интеграл 
находится с помощью формулы Эйлера 
(обозначение Sinc (x) есть отношение sin (x)/x. В системе MATLAB имеется встроенная М-функция sinc(x) = sin(pi*x)/(pi*x) для вычисления этого соотношения, однако можно воспользоваться своей функцией sinc1(x)).
Максимальное значение модуля спектральной плотности наблюдается на нулевой частоте и равно S max =2.18e-4 В/Гц (рисунок 1.8). Первый нуль бокового (главного) лепестка появляется на частоте F 0 = 4375 Гц (на рисунке 1.8 частотная ось имеет масштаб Гц). Произведение частоты первого нуля на длительность сигнала (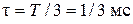
) равно 
.
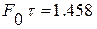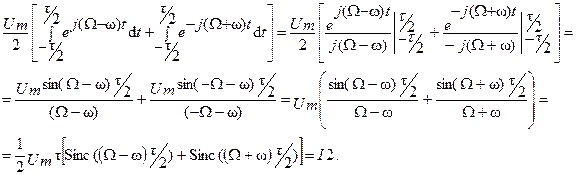
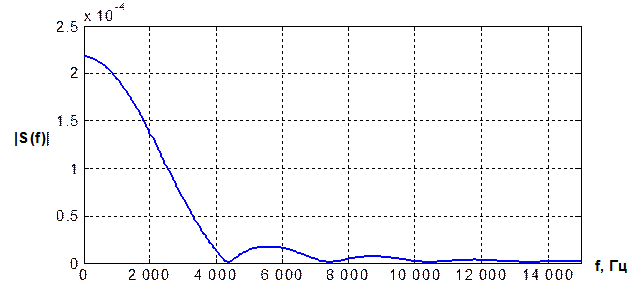
Рисунок 1.8 - Спектральная плотность непериодического сигнала
Ниже приводится два набора команд системы MATLAB (называемые скрипт-файлами), с помощью которых можно вычислить спектральную плотность непериодического сигнала и построить график её модуля. Первый набор реализует вычисление по формулам, полученным в результате аналитического интегрирования.
Uo = 1; Um = 2; T = 1e-3;
tau = T/3; W = 2*pi/T;
f = linspace(0,15e3,300); w = 2*pi*f;
I1 = -Uo*tau*sinc(w*tau/(2*pi));
I2 =1/2*Um*tau*(sinc((W-w)*tau/(2*pi))+sinc((W+w)*tau/(2*pi)));
Sw = I1+I2;
plot(f,abs(Sw)),grid
Второй набор команд вычисляет спектральную плотность сигнала прямым интегрированием по формуле (1.8) методом прямоугольников.
N = 10000;
t = linspace(-tau/2,tau/2,N+1);
i = 1;
for f1=0:50:15000
St(i)=sum(cosinob1(t,Um,T,Uo).*exp(-j*2*pi*f1*t)');
i=i+1;
end
St=St*tau/N;
figure(2)
plot(0:50:15000,abs(St))
При 10000 отсчётах различие между двумя вычисленными спектральными плотностями практически отсутствует (относительная ошибка менее 1е-9).
