При изучении тенденции развития явления во времени часто возникает необходимость определить степень зависимости между динамическими рядами.
Корреляционная связь между уровнями двух динамических рядов называется кросс-корреляцией. Оценка тесноты связи в задачах исследования кросс-корреляции производится с использованием стандартного коэффициента корреляции Пирсона. Однако применение традиционных методов корреляции и регрессии к анализу зависимости временных рядов имеет определенные особенности.
Особое значение приобретает теоретический, содержательный анализ изучаемых явлений и их возможных взаимосвязей во избежание оценки «ложной корреляции». Однонаправленность трендов и высокое значение коэффициента корреляции вовсе не означает наличие причинно-следственной зависимости между рядами. Поэтому, прежде чем приступать к количественной оценке корреляционной зависимости, необходимо теоретически обосновать ее наличие.
Вторая особенность обусловлена тем, что одним из условий применения корреляционно-регрессионного анализа является независимость наблюдений. В контексте изучения временных рядов – это отсутствие связи между уровнями ряда, т.е. автокорреляции. Наличие тренда (автокорреляции) в анализируемых динамических рядах может существенно исказить оценку. Поэтому для получения адекватного результата, необходимо предварительно исключить тенденцию из анализируемых рядов.
Существует несколько способов исключения автокорреляции (тенденции). Один из них основан на переходе от корреляции уровней ряда к корреляции остатков, отклонений фактических уровней от тренда. При этом:
- определяют форму тренда и производят аналитическое выравнивание каждого из связных рядов;
- рассчитывают отклонения фактических уровней от соответствующих выровненных уровней по каждому ряду;
- определяют численное значение коэффициента корреляции по полученным отклонениям.
Практика показывает, что часто в отклонениях от тренда сохраняется автокорреляция. Прежде чем приступить к расчету коэффициента корреляции по остаткам, необходимо проверить наличие в них автокорреляции.
Наряду с коррелированием остатков, способом обойти автокорреляцию уровней может быть метод коррелирования последовательныхразностей или тех цепных показателей динамических рядов, которые являются константами их трендов. Данный подход к исключению автокорреляции вполне оправдан. На длительном временном отрезке искажение корреляции при наличии тренда может быть весьма существенным, благодаря кумулятивному эффекту. В разностях между соседними уровнями воздействие тренда незначительно, т. к. в большей мере они отображают влияние колеблемости.
Еще один прием устранения автокорреляции основан на включении времени в уравнение регрессиив качестве аргумента. Математически доказано, что непосредственное введение в уравнение регрессии фактора времени устраняет автокорреляцию, аналогично использованию отклонений фактических уровней от тренда. Простота реализации этого подхода явилась причиной его широкого применения в практических исследованиях.
В рамках курсового проекта студентам будут предложены для анализа два динамических ряда. Вспомним, что в данном учебном пособии вначале были предложены два динамических ряда, содержащие данные о выезде россиян за границу и их среднедушевых доходах по годам. Очевидно, что динамика выезда за границу зависит от материального положения граждан, а, следовательно, можно рассмотреть корреляционную зависимость между динамическими рядами.
Для демонстрации методов оценки связи между временными рядами создадим новый рабочий лист, на котором будут расположены данные по двум динамическим рядам с 2001 по 2010 год (рис. 6.1) и сделаем его активным.
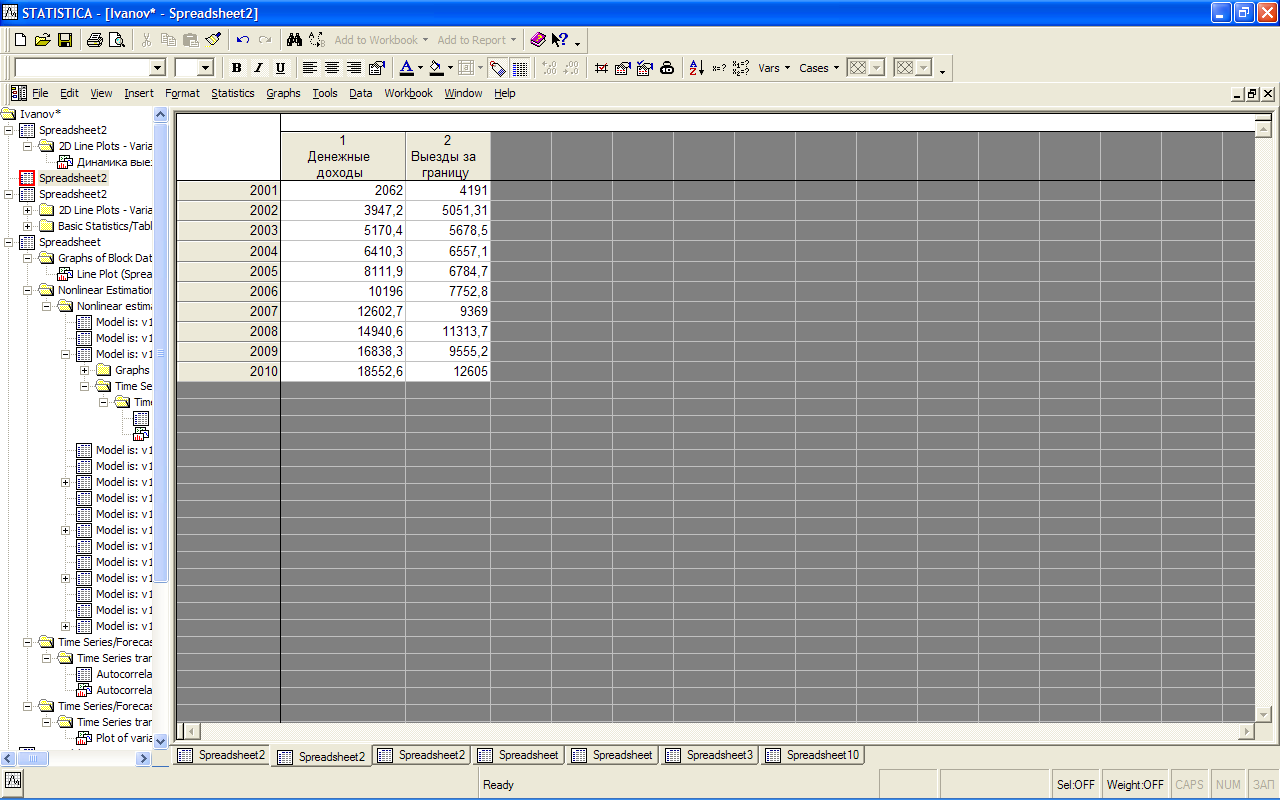
Рис. 6.1. Динамические ряды, подготовленные для оценки автокорреляции
При изучении связи между временными рядами следует помнить, что между изменением уровней одного ряда, как отклика на изменение уровней другого, может существовать определенный временной лаг.
Коэффициенты кросс-корреляции на основе отклонений от трендов в STATISTICA рассчитываются точно так же, как и коэффициенты автокорреляции. Только на закладке Autocorrs. выбирается кнопка Crosscorrelations. Напомним, что это осуществляется с помощью меню Statistics/Advanced Linear/Nonlinear Models/Time Series Forecasting. В качестве переменных выбирается сразу оба динамических ряда (рис. 6.2). Поле Number of lags =4 (рис. 6.3). После нажатия кнопки Crosscorrelations система предложит выбрать переменную, которая является фактором в уравнении. Необходимо теоретически обосновать, какой из динамических рядов является признаком-фактором, а какой признаком-результатом, т.е. обосновать причинно-следственную связь. При этом существую случаи взаимного влияния явлений, при которых выбор признака-фактора не важен. В нашем случае это «Выезды за границу» (рис. 6.4), так как переменная «Денежные доходы» выбрана в предыдущем окне (выделена, см. рис. 6.3) в качестве зависимой.
После нажатия кнопки ОК, система строит таблицу с рассчитанными коэффициентами кросс-корреляции и их стандартными ошибками (рис. 6.5) и графическое изображение, интерпретация которого схожа с графическим изображением коэффициентов автокорреляции (рис. 6.6).
Рис. 6.2. Выбор переменных для построения коэффициентов кросс-корреляции
Рис. 6.3. Окно построения коэффициентов кросс-корреляции
Рис. 6.4. Выбор факторной переменной
Рис. 6.5. Таблица коэффициентов кросс-корреляции
Рис. 6.6. Графическое изображение коэффициентов кросс-корреляции
На основании рассчитанных коэффициентов кросс-корреляции определяется лаг наиболее существенной взаимосвязи между динамическими рядами, то есть тот лаг, которому соответствует максимальный значимый коэффициент кросс-корреляции. В нашем случае максимально значение достигается при 
и составляет r = 0,967641. Однако построение факторно-временных функций на нулевым лаге не имеет практического смысла, поэтому стоит рассмотреть значимую зависимость при 
, r = 0,684897.
При этом минусовой лаг говорит о том, что переменная «Денежные доходы» отстает от переменной «Выезды за границу» на один период, а, значит, является признаком-фактором в возможном уравнении, в отличие от нашей гипотезы. Это можно интерпретировать как желание зарабатывать больше для осуществления поездок за границу.
Описанный выше прием непосредственного включения в уравнение связи фактора времени, позволяет не только оценить зависимость между рядами, но и получить модель для прогнозирования:
,
или
где i – лаг наибольшей взаимосвязи между рядами; z – признак-фактор (переменная «Выезды за границу»); y – признак-результат (переменная «Денежные доходы»).
Очевидно, что в нашем случае уравнение будет иметь вид 
.
Так как здесь имеет место сдвиг динамических рядов, необходимо создать новый рабочий лист со смещенными данными и удалить строки с неполными данными. Также на листе следует создать переменную с фактором времени (рис. 6.7), а затем уже известным способом построить факторно-временную модель (рис. 6.8).
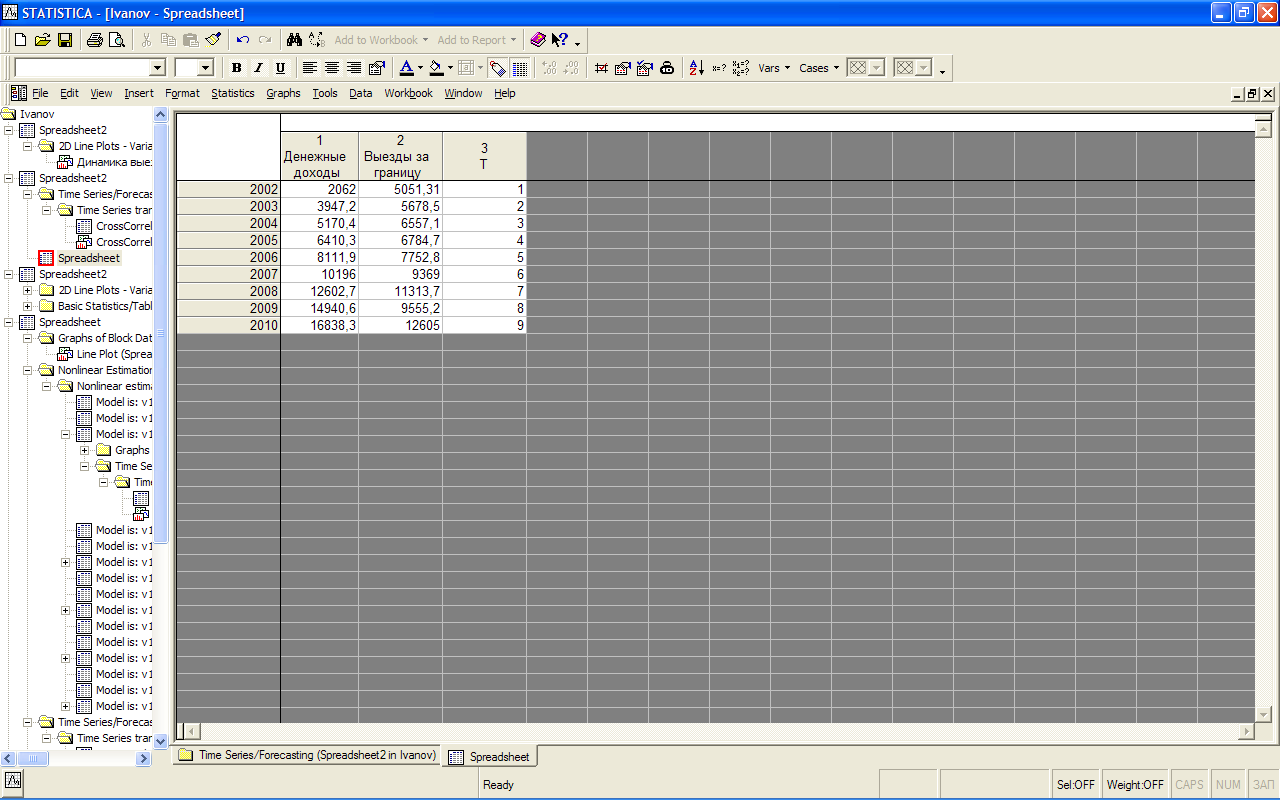
Рис. 6.7. Окно с новым рабочим листом для построения факторно-временной модели
Рис. 6.8. Расчет параметров факторно-временной функции
При условии статистической значимости уравнения и параметров модель может быть использована для прогнозирования. В нашем случае этого не наблюдается.
Отметим, что при возможности прогнозирование все действия аналогичны прогнозированию с помощью трендовых моделей, но не стоит забывать о сокращение числа уровней ряда.
