Как уже отмечалось, проблема выбора формы кривой – одна из основных проблем, с которой сталкиваются при выравнивании ряда динамики. Решение этой проблемы во многом определяет результаты экстраполяции тренда. В большинстве специализированных программ для выбора лучшего уравнения тренда предоставляется возможность воспользоваться несколькими критериями, приведем некоторые из них:
1. Минимальное значение среднеквадратической ошибки тренда:
, (3.11)
где 
– фактические значения уровней ряда динамики;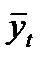 
– значения уровней ряда, определенные по уравнению тренда; n –число уровней ряда; m –число параметровв уравнении тренда.
2. Минимальное значение остаточной дисперсии:
. (3.12)
3. Минимальное значение средней ошибки аппроксимации (MAPE – Mean Absolute Percentage Error):
. (3.13)
4. Минимальное значение среднего абсолютного отклонения MASD – Mean Absolute Derivation):
. (3.14)
5. Максимальное значение коэффициента детерминации
, (3.15)
где 
– общая дисперсия; 
– остаточная дисперсия.
6. Максимальное значение F- критерия Фишера:
: 
. (3.16)
В данном пособии для идентификации тренда используется формальный метод, который основывается на использовании численного критерия. В качестве такого критерия рассматривается максимальный коэффициент детерминации, который показывает, какая доля общей дисперсии результативного признака обусловлена вариацией признака – фактора.
Напоминаем, что значение коэффициента детерминации необходимо было выписать (см. раздел 3.3.). Если этого не было сделано, то нужно рассчитать его значение по формуле (3.15).
Далее необходимо проанализировать выбранную модель тренда с точки зрения ее адекватности реальным тенденциям исследуемого временного ряда через оценку надежности полученных уравнений трендов по F -критерию Фишера и параметров уравнений трендов по t -критерию Стьюдента.
Поскольку F -критерий основан на соотношении факторной и остаточной дисперсий, то вполне логично его использование для оценки качества модели. Если объясненная дисперсия существенно больше необъясненной, это означает, что в уравнение тренда фактор времени учтен, верно. Статистическая значимость уравнения одновременно означает статистическую значимость коэффициента детерминации.
Если 
, то делается вывод о статистической значимости уравнения в целом.
Рассмотрим оценку значимости уравнения на примере линейного тренда. Согласно расчетной таблице (см. рис. 3.18) 
, а для определения теоретического значения F -критерия необходимо воспользоваться встроенным вероятностным калькулятором STATISTICA. Для этого запускаем процедуру Statistics/Probability Calculator/Distributions (рис. 3.27). В появившемся окне в левом столбце выбираем распределение Фишера F(Fisher), далее ставим метку в поле (1-Cumulative p), далее в поле p (теоретический уровень значимости) ставим 0,05 (поскольку установленная вероятность равна 95%), в поле df1 заносим число степеней свободы трендового уравнения (равно числу параметров трендового уравнения, для линейного – 2), в поле df2 заносим число степеней свободы остаточной дисперсии (число уровней ряда минус число параметров уравнения, в нашем случае – 8) и нажимаем кнопку Compute. В поле F появляется теоретического значения F -критерия (в нашем случае – 4,458970) (рис. 3.28). Отметим, что число степеней свободы для каждого уравнения также можно взять из таблицы дисперсионного анализа (см. рис. 3.18).
Таким образом, линейную модель тренда следует считать статистически значимой. То же самое необходимо проделать и для остальных
моделей.
Рис. 3.27. Запуск процедуры Statistics/Probability Calculator/Distributions
Рис. 3.28. Вероятностный калькулятор с расчетом критерия Фишера
Оценка статистической значимости параметров модели означает проверку нулевых гипотез о равенстве параметров генеральной совокупности нулю, т.е.:
Н0: 
=0, Н0: 
=0.
Проверка производится с использованием t -статистики, которая в этом случае представляет собой отношение значения параметра к его стандартной (среднеквадратической) ошибке S:
и 
, (3.17)
поскольку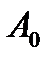 
= 0 и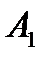 
= 0, то
, 
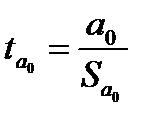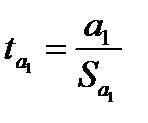, (3.18)
где 
– стандартная ошибка параметра 
: 
= 
; 
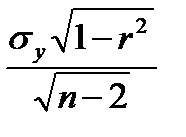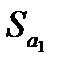– стандартная ошибка параметра 
: 
= 
.
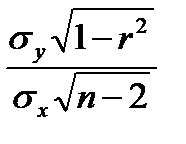Фактические значения t -критерия сравниваются с табличными (с учетом уровня значимости α и числа степеней свободы. Параметры признаются статистически значимыми, т.е. сформированными под воздействием неслучайных факторов, если t факт > t табл.
Фактические значения t -критерия можно взять из таблицы расчета параметров уравнения тренда (см. рис. 3.17) в соответствующем столбце, там же подписано и значения числа степеней свободы. Для получения теоретических значений t -критерия опять воспользуемся встроенным вероятностным калькулятором, однако теперь в столбце слева выберем распределение Стьюдента t (Student). Ставим метку в полях (1-Cumulative p) и Two-tailed, далее в поле p (теоретический уровень значимости) ставим 0,05 (поскольку установленная вероятность равна 95%), в поле df заносим число степеней свободы и нажимаем кнопку Compute. В поле t появляется теоретического значения t -критерия (в нашем случае – 2,306004) (рис. 3.29). Поскольку t факт для параметров линейного уравнения соответственно равны 5,66455 и 10,08865, то их следует признать статистически значимыми.
То же самое следует определить и для остальных трендовых моделей.
Рис. 3.29. Вероятностный калькулятор с расчетом критерия Стьюдента
Результаты оценки уравнения могут быть разными. Возможен вариант, когда уравнение в целом статистически значимо, а некоторые параметры уравнения незначимы. Это означает, что описанная зависимость может служить основой для принятия некоторых управленческих решений, но полученное уравнение тренда нельзя использовать для прогнозирования. Уравнение признается моделью и может быть использовано в целях прогнозирования, если статистически значимы и параметры, и уравнение в целом.
Система дает подсказки пользователю:
1) красным цветом выделяются строки, соответствующие статистически значимым параметрам уравнения тренда;
2) таким же образом выделяется значимость F -критерия в строке Regression дисперсионного анализа.
После анализа значимости уравнений тренда и параметров уравнений, а также выбора критерия сравнения (коэффициент детерминации), рекомендуется составить следующую таблицу (табл. 3.3)
Таблица 3.3
Итоговые характеристики построенных уравнений тренда
| № | Модель | Уравнение | 
| Значимость уравнения | Значимость параметров уравнения |
| Линейная |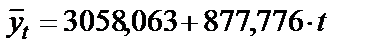 
| 0,927 | + | + | |
| Полином 2-ой степени | 
| 0,932 | + | - | |
| Логарифмическая | 
| 0,802 | + | + | |
| Степенная | 
| 0,893 | + | + | |
| Полином 3-ей степени | 
| 0,933 | + | - |
Сопоставив значения коэффициентов детерминации для различных типов кривых можно сделать вывод о том, что для исследуемого динамического ряда лучшей форма тренда будет полином 3-ей степени, однако анализ значимости параметров уравнения говорит о невозможности использования полиномов 2-й и 3-й степени для прогнозирования. Исходя из этого рассматривать стоит только три модели, которые имеет значимые оценки уравнения и параметров уравнения, а наибольший коэффициент детерминации имеет линейная.
