В ньютоновской механике масса считается независящей от скорости, однако это вовсе не означает, что она должна оставаться постоянной в процессе движения тела. Она может меняться, например, при обмене веществом между телом и оружающей средой. Типичным примером движения тела переменной массы является реактивное движение. В процессе работы установленного на ракете двигателя продукты сгорания топлива выбрасываются через сопло двигателя, и масса ракеты постепенно уменьшается.
Основное уравнение динамики материальной тела переменной массы было получено И.В. Мещерским. Рассмотрим систему, состоящую из поступательно движущегося тела переменной массы и отделяющихся от него частиц (рис.2.14). В момент времени 
масса тела равна 
, его скорость 
, полный импульс системы равен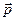 
. От тела отделяются частицы со скоростью 
.За время 
масса отделившихся частиц составила 
, а масса тела стала равна 
, скорость тела увеличилась до значения 
, тогда изменение импульса системы за время равно 
. Раскрыв скобки и пренебрегая величиной 
, получаем 
, или 
, где 
– скорость отделяющихся частиц по отношению к рассматриваемому телу (относительная скорость). Подставив последнее выражение в закон изменения импульса (2.5), получим уравнение Мещерского:
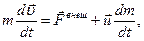
векторная величина 
имеет размерность силы и называется реактивной силой. Положив в этом уравнении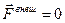 
, получим формулу Циолковского для движения ракеты под действием одной только реактивной тяги:
где 
- скорость истечения продуктов сгорания из сопла ракеты, измеренная относительно ракеты. Если начальная скорость ракеты равна нулю, а траектория – прямая линия, то скорости и направлены противоположно, и в проекции на направление движения ракеты получаем 
или 
.
Если 
–стартовая скорость ракеты, а 
– конечная масса ракеты после окончания работы двигателей вследствие выгорания всего топлива, 
- масса топлива, тогда интегрируя последнее выражение, получим максимальную скорость ракеты: 
или 
Эта формула называется формулой Циолковского.
