Всякое реальное тело под действием приложенных к нему сил деформируется,
т.е.изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации наблюдаются в том случае, если сила, обусловившая деформацию, не превосходит некоторый предел, называемый пределом упругости. Тело, в котором возникают только упругие деформации, называется абсолютно упругим.
Если после прекращения действия сил форма и размеры тела не восстанавливаются, говорят о неупругой деформации.
Рассмотрим пружину, имеющую в недеформированном состоянии длину 
, и приложим к ее концам равные по величине, противоположно направленные силы 
и 
(рис.2.6). Под действием этих сил пружина растянется на некоторую величину 
, после чего наступит равновесие. В состоянии равновесия внешние силы и будут уравновешены упругими силами, возникшими в пружине в результате деформации. При небольших деформациях удлинение пружины оказывается пропорциональным растягивающей силе:
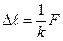(2.18)
- это закон Гука. Здесь 
- коэффициент жесткости пружины.
Упругие натяжения возникают во всей пружине. Любая часть пружины действует на другую часть с силой, определяемой формулой (2.18). Поэтому, если разрезать пружину пополам, та же по величине упругая сила будет возникать в каждой из половин при в два раза меньшем удлинении. Таким образом, при заданных материале пружины и размерах витка величина упругой силы определяется не абсолютным удлинением пружины , а относительным удлинением 
При сжатии пружины также возникают упругие натяжения, но другого знака. Обобщим формулу (2.18) следующим образом. Закрепим один конец пружины неподвижно (рис.2.7), а удлинение пружины будем рассматривать как координату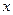 
другого конца, отсчитываемую от его положения, отвечающего недеформированной пружине. Под 
будем понимать проекцию на ось 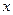упругой силы 
. Тогда можно записать:
. (2.19)
Из рис.2.7 видно, что проекция упругой силы на ось 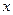и координата 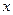всегда имеют разные знаки.
Однородные стержни ведут себя при растяжении или одностороннем сжатии подобно пружине. Если к концам стержня приложить направленные вдоль его оси силы и 
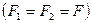, действие которых равномерно распределено по всему сечению, то длина 
стержня получит положительное (при растяжении) или отрицательное (при сжатии) приращение (рис.2.8).Деформация стержня характеризуется относительным изменением длины: 
Экспериментально доказано, что для стержней из данного материала относительное удлинение при упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня:
. (2.20)
Коэффициент пропорциональности a называется коэффициентом упругой податливости.
Величина, равная отношению силы к площади поверхности, на которую действует сила, называется напряжением. В результате взаимодействия частей тела друг с другом напряжение передается во все точки тела и весь объем стержня оказывается в напряженном состоянии. Если сила направлена по нормали к поверхности, напряжение называется нормальным и обозначается s. Если сила направлена по касательной к поверхности, возникает тангенциальное напряжение 
.
В выражении (2.20) 
, поэтому 
.
Величина, обратная упругой податливости, называется модулем Юнга 
С учетом сказанного, 
. Модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение было бы равно единице.
Решив записанные уравнения относительно F получаем: 
.
Это закон Гука для стержня.
