Центром масс (инерции) механической системы называется точке  , радиус-вектор которой равен отношению суммы произведений масс всех материальных точек системы на их радиус-векторы к массе всей системы:
, радиус-вектор которой равен отношению суммы произведений масс всех материальных точек системы на их радиус-векторы к массе всей системы:
 (2.12)
(2.12)
где  и
и  - масса и радиус-вектор
- масса и радиус-вектор 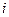 -той материальной точки,
-той материальной точки,  -общее число этих точек,
-общее число этих точек,  – суммарная масса системы. Если радиус- векторы проведены из центра масс
– суммарная масса системы. Если радиус- векторы проведены из центра масс  , то
, то  .
.
Таким образом, центр масс – это геометрическая точка, для которой сумма произведений масс всех материальных точек, образующих механическую систему, на их радиус-векторы, проведенные из этой точки, равна нулю.
Продифференцировав формулу (2.12) по времени, получаем выражение для скорости центра масс: 
Тогда импульс системы равен произведению ее массы на скорость центра масс:  . Подставив это выражение в основное уравнение динамики поступательного движения твердого тела, имеем:
. Подставив это выражение в основное уравнение динамики поступательного движения твердого тела, имеем:
 (2.13)
(2.13)
- центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору приложенных к системе внешних сил.
Уравнение (2.13) показывает, что для изменения скорости центра масс системы необходимо, чтобы на систему действовала внешняя сила. Внутренние силы взаимодействия частей системы могут вызвать изменения скоростей этих частей, но не могут повлиять на суммарный импульс системы и скорость ее центра масс.
Если механическая система замкнутая, то 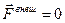 и скорость центра масс не изменяется с течением времени. Таким образом, центр масс замкнутой системы либо покоится, либо движется с постоянной скоростью относительно инерциальной системы отсчета. Это означает, что с центром масс можно связать систему отсчета, и эта система будет инерциальной.
и скорость центра масс не изменяется с течением времени. Таким образом, центр масс замкнутой системы либо покоится, либо движется с постоянной скоростью относительно инерциальной системы отсчета. Это означает, что с центром масс можно связать систему отсчета, и эта система будет инерциальной.
 2.6. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ
2.6. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ
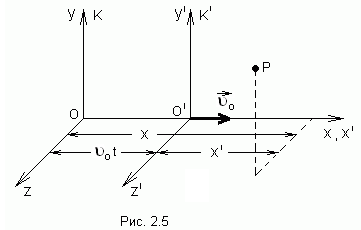
Рассмотрим две системы отсчета, движущиеся друг относительно друга с постоянной скоростью  . Одну из систем, обозначенную на рис.2.5 буквой
. Одну из систем, обозначенную на рис.2.5 буквой  , будем условно считать неподвижной. Тогда вторая система
, будем условно считать неподвижной. Тогда вторая система  будет двигаться прямолинейно и равномерно. Выберем координатные оси
будет двигаться прямолинейно и равномерно. Выберем координатные оси 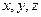 системы
системы  и оси
и оси 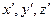 системы
системы  так, чтобы оси
так, чтобы оси 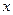 и
и  совпадали, а оси
совпадали, а оси  и
и  , а также
, а также  и
и  были параллельны друг другу.
были параллельны друг другу.
Найдем связь между координатами 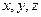 некоторой точки
некоторой точки  в системе
в системе  и координатами
и координатами 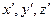 той же точки в системе
той же точки в системе  . Если начать отсчет времени с того момента, когда начала координат обеих систем совпадали, то, как следует из рис.2. 5,
. Если начать отсчет времени с того момента, когда начала координат обеих систем совпадали, то, как следует из рис.2. 5,
 ,
,  .
.
В классической механике считается, что время в обеих системах течет одинаковым образом,  . Тогда получаем совокупность четырех уравнений, называемых преобразованиями Галилея:
. Тогда получаем совокупность четырех уравнений, называемых преобразованиями Галилея:
 ,
,  ,
,  . (2.14)
. (2.14)
Продифференцировав выражения (2.14) по времени, найдем связь между скоростями точки  по отношению к системам отсчета
по отношению к системам отсчета  и
и  :
:
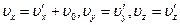 . (2.15)
. (2.15)
В векторной форме  . (2.16)
. (2.16)
Формулы (2.15) и (2.16) выражают правило сложения скоростей в классической механике. При этом следует помнить, что выражения (2.15) справедливы лишь в случае выбора осей, показанных на рис.2.5. Выражение (2.16) справедливо при любом выборе осей. Продифференцировав (2.16) по времени, получаем:
 (2.17)
(2.17)
- ускорение тела во всех инерциальных системах отсчета одинаково. Это означает, что и силы, действующие на тело в инерциальных системах отсчета одинаковы. Следовательно, уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой, т.е. инвариантны к преобразованиям Галилея. С механической точки зрения все инерциальные системы отсчета совершенно эквивалентны, ни одной из них нельзя отдать предпочтение перед другими. Это означает, что никакими механическими опытами, проведенными в пределах данной системы отсчета, нельзя установить, находится ли она в состоянии покоя или движется прямолинейно и равномерно. Эти положения носят название принципа относительности Галилея.
СИЛЫ
В современной физике различают четыре вида взаимодействий: гравитационное (вызванное всемирным тяготением), электромагнитное (осуществляемое через электрические и магнитные поля), сильное или ядерное (обеспечивающее связь частиц в атомном ядре) и слабое (проявляющееся при распаде элементарных частиц).
В классической механике имеют дело с гравитационными и электромагнитными силами, а также с упругими и силами трения. Два последних вида сил определяются характером взаимодействия между молекулами вещества и имеют электромагнитное происхождение.
Гравитационные и электромагнитные силы являются фундаментальными, их нельзя свести к другим, более простым силам. Упругие силы и силы трения не являются фундаментальными.






