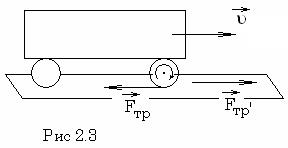
Механическое действие тел друг на друга всегда является их взаимодействием. Если тело 1 действует на тело 2, то при этом обязательно тело 2 действует на тело 1. Так, например, на ведущие колеса электровоза (рис.2.3) действуют со стороны рельсов силы трения покоя, направленные в сторону движения электровоза. Сумма этих сил и есть сила тяги электровоза. В свою очередь, ведущие колеса действуют на рельсы силами трения покоя, направленными в противоположную сторону.
Количественное описание механического взаимодействия было дано Ньютоном в его третьем законе динамики. Для материальных точек этот закон формулируется так:
Две материальные точки действуют друг на друга с силами, равными по величине и направленными противоположно по прямой, соединяющей эти точки (рис.2.4): 
. Третий закон справедлив не всегда. Он выполняется строго в случае контактных взаимодействий, а также при взаимодействии находящихся на некотором расстоянии друг от друга покоящихся тел.
Перейдем теперь от динамики отдельной материальной точки к динамике механической системы, состоящей из 
материальных точек. Для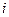 
-той материальной точки системы, согласно второму закону Ньютона (2.5), имеем:
. (2.6)
Здесь 
и 
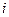- масса и скорость -той материальной точки, 
- сумма всех действующих на нее сил.
Силы, действующие на механическую систему, делятся на внешние и внутренние. Внешние силы действуют на точки механической системы со стороны других, внешних тел. Внутренние силы действуют между точками самой системы. Тогда силу в выражении (2.6) можно представить в виде суммы внешних и внутренних сил:
, (2.7)
где 
– результирующая всех внешних сил, действующих на 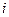-тую точку системы; 
-внутренняя сила, действующая на эту точку со стороны 
-й. Подставим выражение (2.7) в (2.6):
, (2.8)
просуммировав левые и правые части уравнений (2.8), записанных для всех материальных точек системы, получаем
. (2.9)
По третьему закону Ньютона силы взаимодействия 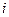-той и -й точек системы равны по модулю и противоположны по направлению 
.
Поэтому сумма всех внутренних сил в уравнении (2.9) равна нулю:
. (2.10)
Векторная сумма всех внешних сил, действующих на систему,
называется главным вектором внешних сил
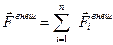. (2.11)
Поменяв в выражении (2.9) местами операции суммирования и дифференцирования и учитывая результаты (2.10) и (2.11), а также определение импульса механической системы (2.3), получаем 
. Это основное уравнение динамики поступательного движения твердого тела: скорость изменения импульса механической системы равна векторной сумме приложенных к ней сил.
Если система замкнутая,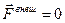 
, то 
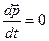и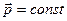 
- в замкнутой механической системе полный импульс сохраняется. Это закон сохранения импульса.
