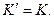Ми бачили в § 1, що при повороті осей координат кожна з величин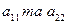 
змінюється (перетворюються у нові величини 
), але їх сума залишається незмінною:
Говорять, що 
являється інваріантом перетворення повороту осей координат.
Взагалі будь-яка функція
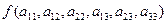
Від коефіцієнтів полінома-рівняння лінії називається інваріантою при перетворенні прямокутних координат, якщо значення цієї функції залишається незмінним при переході від однієї прямокутної системи координат до іншої.
Обмежимося розглядом тих інваріантів перетворення прямокутної системи координат в прямокутну, які розв’язують задачу визначення виду лінії та параметрів її канонічного рівняння.
1. Інваріанти перетворення повороту осей координат. Перетворимо ліву частину рівняння
за формулами
ми отримуємо рівняння, в котрому нові коефіцієнти 
виражаються через коефіцієнти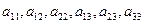 
за наступними формулами
а) З рівності 
слідує, що вільний член рівняння кривої – це інваріант перетворення повороту осей координат.
б) Склавши почленно рівності (1) та (3), маємо:
Таким чином, сума коефіцієнтів при 
- це інваріант перетворення повороту осей координат.
в) Віднявши від рівності (1) рівність (3), маємо:
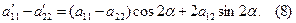
Помноживши на 2 ліву та праву частини рівності (2), маємо:
Підносимо до квадрату обидві частини рівностей (8) та (9) та складаємо результати, в результаті отримуємо:
або
звідки на основі рівності (7) слідує, що
або
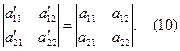
Визначник 
, (11)
який називають дискримінантом старших членів рівняння кривої другого порядку, являється, таким чином, інваріантою повороту осей координат.
г) Підносячи ліві та праві частини рівностей (4) та (5) до квадрату, маємо:
тобто, сума квадратів коефіцієнтів при х та у буде інваріантою повороту.
д) Визначник
Називається дискримінантом рівняння кривої другого порядку, а також інваріантою перетворення повороту осей координат.
Позначимо отримані п’ять інваріантів перетворення повороту осей координат так:
2. Інваріанти перетворення переносу початку координат. Перетворимо ліву частину рівності
використовуючи формули
отримаємо нове рівняння виду:
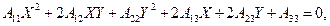
де
З рівностей (14) ми бачимо, що коефіцієнти при х2, ху, у2 будуть інваріантами перетворення перенесення початку координат. Можна показати, що
буде також інваріантою цього перетворення.
3. Інваріанти загального перетворення осей координат. Так як
інваріанти перетворення паралельного переносу, то
Будуть також інваріантами цього перетворення, а значить, інваріанти 
будуть загальними для перетворень повороту та перетворення переносу, вони будуть, таким чином, інваріантами загального перетворення прямокутної системи координат в прямокутну, що виконується з використанням формул:
Будемо ці інваріанти позначати надалі через І1, І2, І3:
Коефіцієнти характеристичного рівняння
Виступають інваріантами І1 та І2 і, значить, його можна записати у вигляді:
4. Семиінваріанта (напівінваінта). Функція К виду:
буде інваріантою перетворення повороту осей координат, так як вона виражається через раніше знайдені інваріанти. Насправді:
Що стосується перетворення перенесення початку координат, то К, взагалі кажучи, змінюється.
В силу цього функцію К називають семиінваріантою (напівінваріантою).
Однак легко можна впевнитися в тому, що для лінії третього типу функція К буде інваріантою також і для перетворення перенесення початку координат, а значить, і для загального перетворення.
Розглянемо перетворення рівняння кривої другого типу:
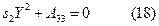
і перетворимо його перенесенням початку координат за формулами:
Отримаємо рівняння:
Підрахуємо значення функції К для рівнянь (18) та (19):
Таким чином, 
