Кривими другого порядку називають такі лінії, рівняння яких в декартових координатах будуть рівняннями ІІ степеню. До ліній ІІ порядку відносяться вже відомі нам конічні перетини:
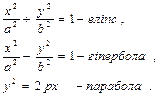
Загальне рівняння кривої другого порядку відносно змінних х та у має вигляд:
(де хоча б один із коефіцієнтів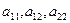 
відмінний від нуля, так як інакше рівняння було би рівнянням першого степеню).
Коефіцієнти позначені однією і тією же буквою з двома позначками для надання симетричності формулам. З цією же метою коефіцієнти при ху, х та у взяті з множником 2.
Значок 1 вказую на те, що в даний член входить співмножник х, значок 2 вказує на присутність в даному члені співмножника у і значок 3 – що в члені відсутній другий співмножник.
При такому позначені коефіцієнтів мають місце рівності:
Відомо, що одна і таж лінія має різні рівняння в залежності від її положення відносно системи координат. Нехай нам задана лінія рівнянням:
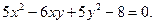
Знайдемо рівняння цієї лінії відносно системи координат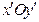 
, отриманої з початкової системи шляхом повороту її на кут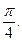 
Формули повороту для цього випадку мають вигляд:
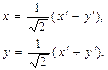
Підставивши ці значення х та у в початкове рівняння даної лінії, ми отримаємо її рівняння відносно нової системи координат:
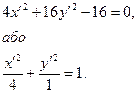
А це і є відоме канонічне рівняння еліпса.
В загальній теорії кривих другого порядку будемо знаходити рішення наступних задач:
1. Класифікація ліній, що мають рівняння виду (1).
2. Знаходження канонічного рівняння даної кривої та побудова її в початковій системі координат.
3. Вивчення ряду питань, пов’язаних з перетином кривих другого порядку з прямими (асимптотичні напрями, центр, діаметри, дотичні).
