Теорема. Для будь-якої кривої другого порядку існує така прямокутна система координат, відносно якої рівняння цієї лінії не містить в собі члена ху.
Нехай в деякій прямокутній системі координат лінія другого порядку задана рівнянням:
Повернемо осі координат на деякий кут 
; тоді координати усіх точок площини перетворяться за формулами:
Користуючись цими формулами, отримаємо рівняння кривої (1) в новій системі координат.
Для цього замінимо в рівнянні (1) х та у їх значеннями по формулам (2):
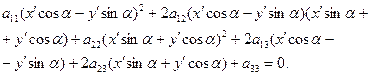
Після перетворення рівняння лінії набере вигляду:
Виберемо тепер кут так, щоб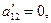 
тобто: 
Розв’язуючи це рівняння, маємо:
Цим теорема доведена, так як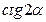 
може приймати будь-яких значень. В рівнянні (10) 
Насправді, якщо б 
то рівності (10) слідувало, що 
і, значить, в повороті осей координат необхідності не має.
Поділивши всі члени рівняння (10) на 
маємо:
Так як дискримінант цього рівняння
воно матиме два дійсних розв’язки: 
За теоремою Вієтта 
, значить 
відмінні від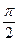 
. Для того, щоб скласти формули повороту осей координат (2), потрібно взяти будь-яке із значень 
і підрахувати за формулами:
Після перетворення рівняння (1) набере вигляду:
Приклад 1.
Спростити рівняння 
та побудувати лінію, зберігаючи на малюнку початкову систему координат.
Розв’язання.
В даному прикладі
Визначимо тангенс кута повороту з рівняння (12):
Беремо 
.
Обчислимо за формулами (13) 
Складемо формули повороту осей координат:
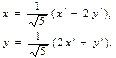
Перетворивши за даними формулами рівняння даної лінії, отримаємо:
або
Дана лінія – еліпс з півосями 
Побудуємо цей еліпс, зберігаючи початкову систему координат
(мал.1).
Вправа. Спростити рівняння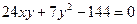 
та побудувати
Відповідну йому криву, зберігаючи початкову систему координат.
Складання рівняння(14) кривої (1) відносно нової системи координат можна виконати простіше. Звернемо увагу, по-перше,
що: 
в чому легко впевнитися, склавши рівняння (4) та (6).
Перетворимо рівність (10) до вигляду:
Позначивши ці відношення через «s», маємо систему:
Ця система лінійних однорідний рівнянь відносно невідомих 
має розв’язки, відмінні від нульових (нульових розв’язків у системи немає, так як одночасно не можуть бути нулями) при умові, що визначник дорівнює нулю, тобто:
або в розгорнутому вигляді:
Це рівняння називається характеристичним.
Його дискримінант
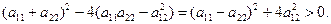
Значить, рівняння (18) має дійсні корені 
. Взявши один із них, наприклад 
, можна з рівнянь 
або 
знайти 
- кут повороту осей координат
Якщо взяти значення кореня 
, то отримаємо:
Покажемо, що напрями 
взаємно перпендикулярні; для цього знайдемо:
За теоремою Вієтта для рівняння 
,
ось чому
За теоремою Вієтта для рівняння маємо: 
,
а так як 
то
Тепер не важко підрахувати коефіцієнти 
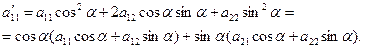
Але так як 
задовольняють рівнянням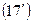 
,
то
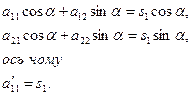
Із рівності (20) отримуємо, що 
Рівняння (14) можна тепер записати в наступному вигляді:
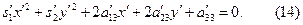
Приклад 2.
Спростіть рівняння (звільніться від члену з добутком ху):
Розв’язок.
1) Складемо характеристичне рівняння:
Розв’язуючи рівняння, знаходимо: 
2) Знайдемо кут повороту осей координат:
3) Складемо формули перетворення повороту осей координат:
4) Перетворимо лінійну частину даного рівняння:
5) Рівняння лінії в новій системі координат матиме вигляд:
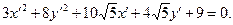
Вправа. Звільнитися від члена з добутком ху у рівнянні кривої:
