Так як коефіцієнти рівняння
Обчислюються через коефіцієнти вихідного рівняння 
то можливі три принципово нові випадки, у відповідності з якими всі криві другого порядку розбиваються на лінії трьох типів.
І тип – коефіцієнти при квадратах обох змінних у рівнянні (1) відмінні від нуля:
ІІ тип – один із коефіцієнтів при квадратах змінних рівний нулю, але коефіцієнт при першому степені тієї же змінної відмінний від нуля, наприклад:
ІІІ тип - один із коефіцієнтів при квадратах змінних рівний нулю і коефіцієнт при першому степені тієї же змінної також дорівнює нулю, наприклад:
Розглянемо спрощення кривої кожного типу окремо:
1. Криві першого типу. Якщо 
рівняння кривої матиме вигляд:
Групуючи члени з однойменними змінними та доповнюючи ці групи до повних квадратів, маємо:
Позначимо вирази в дужках через нові змінні:
що рівносильне перенесенню початку координат у точку
Рівняння (1) набирає вигляду:
Дослідимо, які геометричні образи будуть відповідати рівнянню виду (2) при різних значеннях коефіцієнтів 
а) Нехай одного знаку; тоді рівняння (2) можна звести до канонічного вигляду:
Крива, яка відповідає рівнянню (3), а, значить, і рівнянню (2), це дійсний еліпс.
б) Нехай 
одного знаку, А- протилежного їм, тоді рівняння (2) можна звести до канонічного вигляду:
Криву, яка відповідає рівнянню (4), а, значить, і рівнянню (1), називатимемо уявним еліпсом, так як рівняння (4) не задовольняється дійсними значеннями х та у.
в) Нехай різних знаків, знак А будь-який; тоді рівняння (2) можна звести до канонічного вигляду:
Крива, яка відповідає рівнянню (5), а, значить, і рівнянню (1), буде гіперболою з дійсною віссю 
, якщо (+1) стоїть з правого боку, інакше 
, якщо (-1).
г) Нехай 
одного знаку і А=0; тоді рівняння (2) можна звести до канонічного вигляду:
Це рівняння задовольняється однією парою дійсних значень Х=0,Y=0; таким чином, геометричним образом, який відповідає рівнянню (6) і, значить, рівнянню (1), буде точка.
д) Нехай різних знаків і А=0; тоді рівняння (2) можна звести до канонічного вигляду:
Ліва частина цього рівняння розкладаються на лінійні множники і рівняння (7) розпадається на два лінійних рівняння:
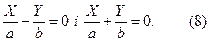
Геометричний образ, який відповідає цьому рівнянню (7),а, значить, і рівнянню (1), буде складатися з двох прямих, що перетинаються (8).
2. Криві другого типу. Якщо 
, то рівняння (1) набирає вигляду:
Групуючи члени з однойменними змінними та доповнюючи групи до повних квадратів, маємо:
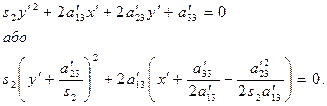
Позначимо вирази в дужках через нові змінні:
що рівносильне перенесенню початку координат в точку
Тоді рівняння (9) набере вигляду:
Розв’язуючи це рівняння відносно Y2, зводимо його до канонічного вигляду:
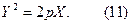
Кривою, що відповідає рівнянню (11), а, значить, і рівнянню (9), буде парабола.
3. Криві третього типу. Якщо 
, то рівняння (1) набирає вигляду:
Перетворенням перенесення початку координат це рівняння можна звести до вигляду:
Розв’язуючи це рівняння відносно Y2,отримуємо рівняння виду:
а) Нехай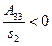 
,тобто рівняння має вигляд:
В цьому випадку геометричний образ, який відповідає цьому рівнянню, буде складатися з двох паралельних прямих:
б) Нехай 
В цьому випадку обидві прямі співпадають і геометричний образ, який відповідає рівнянню (12), складатиметься з двох прямих, що співпадають:
Y=0, та Y=0.
в) Нехай 
В цьому випадку рівняння (13) має вигляд:
та образ, який відповідає рівнянню (13), а значить, і рівнянню (12), називатимемо уявними паралельними прямими:
Дослідивши усі можливі, принципово різні комбінації значень та знаків коефіцієнтів рівняння (1), ми розв’язали першу задачу загальної теорії, а точніше, встановили усі можливі лінії другого порядку.
Дослідження показало, що існують дев’ять різних класів ліній другого порядку (див. звідну таблицю І).
Спосіб спрощення загального рівняння шляхом перетворення координат дає можливість побудувати лінію за її загальним рівнянням в початковій системі координат.
Приклад 1. Спростити рівняння
Та побудувати відповідну йому лінію, зберігаючи початкову систему координат.
Розв’язання. Складемо характеристичне рівняння:
Розв’язавши його, матимемо: s1=16, s2=-9.
2. Знайдемо кут повороту осей координат:
3. Складемо формули перетворення повороту осей координат:
4. Перетворимо лінійну частину даного рівняння:
5. Рівняння лінії після повороту осей координат набере вигляду:
6. Перетворимо дане рівняння групуючи члени та доповнюючи їх до повних квадратів до вигляду:
тобто переносячи початок координат в точку 
відносно повернутої системи координат, перетворимо рівняння лінії відносно нової системи координат 
до вигляду:
7. Зведемо це рівняння до канонічного вигляду:
8. Побудуємо криву (мал.2).
Примітка. При виборі позитивного напряму нової осі 
потрібно керуватися знаками 
|
Приклад 2. Звести рівняння лінії
до найпростішого вигляду та побудувати її.
Розв’язання. 1. Складемо та розв’яжемо характеристичне рівняння:
2. Знайдемо кут повороту осей координат:
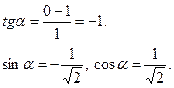
3. Складемо формули повороту осей координат:
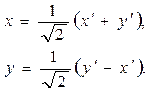
4. Перетворимо лінійну частину даного рівняння:
5. Рівняння лінії після повороту осей координат матиме вигляд:
6. Перетворимо це рівняння до вигляду, групуючи члени та доповнюючи їх до повних квадратів:
Позначивши дужки
тобто, переносячи початок координат в точку 
приведемо рівняння до вигляду:
|
7. Будуємо криву (мал.3).
Приклад 3. Привести рівняння кривої
до найпростішого вигляду.
Розв’язання. 1) 
2) 
3) Після перетворення рівняння набирає вигляду:
4) Перенесемо початок координат в точку 
Рівняння лінії в новій системі координат набирає вигляду:
Таким чином, заданою кривою буде пара прямих, що перетинаються.
5) Побудуємо ці прямі (мал.4).
|
Вправи. Спростити наступні рівняння другого порядку та побудувати відповідні їм криві, зберігаючи при цьому початкову систему координат:
