8.4.1 Операторы поочередно выполняют измерения всех образцов выборки, причем следует уделить особое внимание случайному порядку сбора данных. Рекомендуется определять случайно не только номера измеряемых образцов, но и оператора, выполняющего измерения, причем этот порядок должен быть различным для различных попыток.
8.4.2 Специалист, ответственный за оценивание статистических характеристик измерительного процесса, регистрирует результаты измерений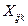 
для всех образцов, операторов и попыток в таблице (Таблица 2). Светло-серым цветом в таблице выделено место для занесения результатов измерений.
8.4.3 Специалист осуществляет предварительные расчеты для анализа сходимости и воспроизводимости (места для занесения результатов предварительных расчетов выделены серым цветом).
Специалист осуществляет расчеты средних значений результатов измерений по формулам (26), (28), (30) и (31). Результаты расчетов заносятся в соответствующие ячейки таблицы «Контрольного листа данных для расчета сходимости и воспроизводимости» (схема заполнения приведена в таблице 2). Ячейки, содержащие данные о размахах, не заполняются при оценивании сходимости и воспроизводимости методом дисперсий.
8.4.4 Результаты измерений и предварительные расчеты специалист регистрирует в «Контрольном листе данных для расчета сходимости и воспроизводимости измерительного процесса» (Приложение Д).
8.4.5 С применением средств вычислительной техники специалист осуществляет расчет оценок дисперсий составляющих изменчивости измерительного процесса.
8.4.5.1 Оценка дисперсии 
средств измерительной техники (сходимость) рассчитывается по формуле:
 ,
| (37) |
где NM (Q - 1) – число степеней свободы.
8.4.5.2 Оценка дисперсии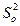 
операторов (воспроизводимости) рассчитывается по формуле:
 ,
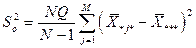| (38) |
где M - 1 – число степеней свободы.
8.4.5.3 Оценка дисперсии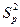 
образцов рассчитывается по формуле:
 ,
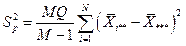| (39) |
где N - 1 – число степеней свободы.
8.4.5.4 Оценка дисперсии 
взаимодействия операторов и образцов рассчитывается по формуле:
 ,
| (40) |
где (N - 1)(M - 1) – число степеней свободы.
Следует заметить, что данная составляющая изменчивости не может быть оценена по методу средних и размахов.
Поскольку дисперсия выборки равна квадрату СКО этой выборки, дисперсии, полученные в п. 8.3.5, могут быть легко преобразованы в соответствующие СКО (для аналогии с методом средних и размахов).
8.4.6 Значимость влияния взаимодействия оператора и образца на изменчивость результатов измерений можно оценить по следующему алгоритму.
8.4.6.1 Специалист рассчитывает соотношение:
 ,
| (41) |
8.4.6.2 По таблице F -распределения (распределения Фишера-Снедекора), приведенной в Приложении И, при уровне значимости a =0,05 определяем критическое значение распределения Fa (k1, k2), где k1 – число степеней свободы большей дисперсии (из и ),
k2 – число степеней свободы меньшей дисперсии (из и ). Числа степеней свободы и равны (N –1)(M –1) и NM (Q –1) соответственно.
8.4.6.3 Если F < Fa (k1, k2), то влияние изменчивости взаимодействия между оператором и деталью признается незначимым, и в дальнейших расчетах не участвует. В противном случае влияние изменчивости взаимодействия между оператором и деталью признается значимым.
8.4.7 Результаты расчета оценок дисперсий, а также вывод о значимости изменчивости взаимодействия между оператором и образцом заносятся в «Протокол анализа сходимости и воспроизводимости измерительного процесса» (Приложение Е).
