Выделить и проанализировать тренд временного ряда. Для этого необходимо выбрать третий временной ряд температуры воды (обозначим через yt,  ). Далее:
). Далее:
1. Применить метод серий, основанный на медиане; метод восходящих и нисходящих серий для проверки наличия тренда.
2. Провести сглаживание ряда динамики методом скользящей средней с интервалом сглаживания l = 7; построить график исходного и сглаженного ряда.
3. С помощью метода наименьших квадратов рассчитать линейное уравнение модели тренда
f (t) = y* (t) = at + b,
где t – условный параметр времени.
Расчет коэффициентов a и b осуществляется по формулам
 ,
,  ,
,
где Т – длина временного ряда.
Следует обратить внимание, что в качестве независимой переменной выступает время, а зависимой переменной является ряд температуры воды.
4. Осуществить расчет коэффициента корреляции rty, его стандартной ошибки sr, коэффициента детерминации h 2 y (t), показывающего вклад тренда в описание дисперсии исходного ряда.
5. Выполнить оценку значимости коэффициента корреляции rty. Для этого выдвигается гипотеза
H0: rty = 0,
для проверки которой рассчитывается критерий Стьюдента
t расч =  .
.
По статистической Таблице 2 Приложения 2 критических точек t - распределения Стьюдента, по заданному уровню значимости aи числу степеней свободы k = n – 2 определяется критическая точка tкр (k, a) двусторонней критической области.
Если | t расч | > tкр, то нулевая гипотеза отвергается. Это означает, что тренд неслучайным образом отличается от нуля и вносит определенный вклад в формирование изменчивости исходного ряда.
6. Вычислить дисперсию отклонения по формуле: 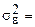
 .
.
7. Оценить величину тренда в 1995 году.
8. Нанести уравнение тренда на график временного ряда и проанализировать полученные результаты. Указать характер тренда (положительный или отрицательный, т.е. рост или падение температуры воды) и возможные физические причины его формирования.
Пример расчетов представлен в таблице 3.
Таблица 3.
Модель линейной регрессии связи температуры воды в декабре в период с1957 по 1993 гг.
в точке 9 (55о с.ш. 30о з.д.), ее параметры и оценка их значимости
| Выборочные характеристики | ||||||||
| Уравнение модели: y* (t) = –0,02 t + 10,95 | ||||||||
| Параметры линейной регрессии | Оценка значимости | Вывод | ||||||
| a | -0,02 | |||||||
| b | 10,95 | |||||||
| rty | -0,42 | s r | 0,15 | t расч | -2,72 | tкр (35; 0,05) | 2,03 | значимый |

| 0,048 | 
| 0,225 | h 2 y (t) | 0,175 | < 0,7 | ||
| se2 | 0,23 | > 20% | ||||||
| se | 0,47 | Sу | 0,52 | 0,67 Sу | 0,35 | se > 0,67 Sу | ||
| Модель среднего качества и требует дополнительного уточнения. Несмотря на значимость коэффициента корреляции, дисперсия ошибки велика. Коэффициент детерминации не подтверждает адекватности выбранной модели тренда. |
Приложение 1






