Проверка гипотезы о нормальном распределении генеральной совокупности

ИНДИВИДУАЛЬНЫЕ РАБОТЫ

по курсу «Математические методы в гидрометеорологии»

I семестр: лекции - 20 ч., практика - 8 ч., КСР – 6 ч.

II семестр: лекции - 16 ч., практика - 6 ч., КСР – 4 ч.

Вид отчетности: зачет.

 

Преподаватель: Цеховая Татьяна Вячеславовна, к. ф. - м. н., доцент

содержание

Индивидуальная работа № 1

Задание 1 Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона (критерию c²).

Задание 2 Основныевыборочные характеристики.

Задание 3 Измерение взаимной зависимости.

Задание 4 Расчет коэффициентов линейного уравнения регрессии.

Задание 5Оценка адекватности регрессионной модели.

Индивидуальная работа № 2

Задание 1 Построение автокорреляционной функции

Задание 2 Анализ временной изменчивости ряда температуры воды.

Приложение 1. ИСХОДНЫЕ ДАННЫЕ К ИНДИВИДУАЛЬНЫМ РАБОТАМ.

Приложение 2. ОСНОВНЫЕ СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ.

Приложение 3. Образец оформления работы в EXcel.

Приложение 4. Установка средств анализа данных пакета MS Excel.

Рекомендуемая литература

Индивидуальные работы

 

К выполнению индивидуальных работ следует приступить после тщательного изучения рекомендованных глав литературы. Для выполнения заданий полезны сведения о расчетных формулах по каждому из разделов дисциплины, а также большой объем справочных данных, которые можно найти, напрмер, в [8].

В результате изучения курса необходимо выполнить две индивидуальные работы. Первая индивидуальная работа состоит из 5 заданий, вторая – из двух.

Ответы на вопросы индивидуальных работ должны быть сформулированы достаточно подробно, чтобы был ясен смысл излагаемого материала, подтвержденный, где это возможно, математическими формулами.

Расчетные задания можно выполнять как с использованием стандартных статистических пакетов (EXCEL, STATISTICA, SPSS и др.) с выводом результатов на печать, так и вручную, с помощью калькулятора.

Все вычисления должны быть представлены в таблицах и рисунках, примеры которых приводятся в соответствующих индивидуальных работах. Остальные результаты и их анализ даются в произвольном виде.

В Приложении 1 приводятся исходные данные о среднемесячной температуре поверхности в разных точках акватории Атлантического океана с 1957 по 1993 гг.

В каждый вариант исходных данных включены 3 временных ряда. Для выполнения индивидуальных работ нужно исследовать или все три ряда, или один из них, что указано в каждом конкретном задании.

В Приложении 2 находятся необходимые таблицы теоретических распределений для проверки статистических гипотез. Можно воспользоваться подобными таблицами, например, в [8].

В Приложении 3 приводится образец оформления заданий индивидуальных работ в MS EXcel.

В Приложении 4 предлагается инструкция по установке средств анализа данных пакета MS Excel.

Номер варианта совпадает с порядковым номером студента в списке группы.

Индивидуальная работа № 1

Задание 1

Проверка гипотезы о нормальном распределении генеральной совокупности

по критерию Пирсона (критерию c²)

Построить графики трех исходных рядов температуры воды (рисунок 1). Визуальный анализ графиков позволяет качественно оценить изменчивость рядов, наличие периодических колебаний и тренда.

Рисунок – 1 Временная изменчивость температуры поверхности океана

в октябре, ноябре и декабре в точке 9 (55° с.ш. 30° з.д.)

 

Для первого из трех предложенных рядов Х _1, Х ₂ и Х ₃ проверить гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона (критерию c²).

Для этого необходимо:

1. Руководствуясь рисунком 1 выдвинуть гипотезу о законе распределения исходных данных.

2. Произвести ранжирование ряда по возрастанию; определить минимальное и максимальное значение выборки:

, ,

п – объем выборки.

Вычислить размах (диапазон) выборки:

R = x _max – x _min.

3. Весь диапазон значений признака [ x _min, x _max] разбить на N интервалов одинаковой длины. Число интервалов N определить по формуле Стерджеса:

N = 1 + [3,322 lg n ] = 1 + [log₂ n ],

где n – объем выборки, [.] – целая часть числа.

Вычислить величину интервалов h = R / N.

4. Определить границы интервалов (a_i, a_{i +1}):

a ₁ = x _min, a ₂ = a ₁ + h = x _min + h, a ₃ = a ₂ + h = x _min+ 2 h, …, a_{N +1} = a_N + h = x _min + Nh.

5. Построить интервальный вариационный ряд, указав абсолютные m_i и относительные w_i частоты. Проверить выполнение условий нормировки для абсолютных и относительных частот.

6. Рассчитать середины x _{( i )} интервалов (a_i, a_{i +1}):

.

7. По имеющемуся интервальному вариационному ряду с помощью Мастера диаграмм MS Excel построить гистограмму и полигон распределения абсолютных частот. Гистограмма представляет собой эмпирическую функцию распределения.

8. Вычислить выборочное среднее и выборочное среднее квадратическое отклонение , где п – объем выборки, N – число интервалов, m_i – абсолютные частоты, 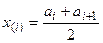– среднее арифметическое концов интервалов.

9. Перейти к нормированным величинам

, ,

причем значение z ₁полагают равным – ¥, а значение z_{N +1} полагают равным + ¥.

10. Вычислить теоретические частоты

m_i' = nP_i,

где п – объем выборки,

P_i = Ф₀(z_{i +1}) – Ф₀(z_i),

Ф₀(z) = , Ф₀(–z) = – Ф₀(z), Ф₀(–¥) = –0,5; Ф₀(¥) = 0,5.

Значения функции Ф₀(z) найти по Таблице 1 Приложения 2.

Замечание 1. Интервалы, содержащие малочисленные эмпирические частоты (m_i < 5), следует объединить, а частоты этих интервалов сложить. В этом случае и соответствующие им теоретические частоты также надо сложить. Если производилось объединение интервалов, то при определении числа степеней свободы по формуле k = N – 3 следует в качестве N принять число интервалов, оставшихся после объединения интервалов.

Замечание 2. Должно выполняться . В случае, если эти величины значительно (более чем на 1) отличаются друг от друга, необходимо ввести дополнительные фиктивные разряды, в которых частоты m_j = 0, а теоретические частоты вычисляются по соответствующей формуле. Количество этих разрядов и их местоположение (в начале или в конце таблицы) должны обеспечивать максимально быстрое выполнение вышеуказанного приближенного равенства.

11. Для того чтобы оценить степень приближения выборочного распределения к теоретической кривой, вычислить наблюдаемое значение критерия c²_набл :

c²_набл = .

12. По Таблице 3 Приложения 2 критических точек распределения c², по заданному уровню значимости a и числу степеней свободы k = N – 3, N – число интервалов, найти критическую точку c²_кр(a; k) правосторонней критической области.

Указания:

а) значение критической точки c²_кр(a; k) можно получить, применяя встроенную статистическую функцию ХИ2ОБР приложения MS Excel.

 

б) значения aуровней значимости выбрать из таблицы согласно номеру варианта:

 

№ варианта
a1	0,01	0,02	0,025	0,05	0,05	0,02	0,01	0,01	0,02
a2	0,05	0,001	0,09	0,025	0,02	0,01	0,05	0,025	0,05
№ варианта
a1	0,025	0,05	0,025	0,01	0,09	0,01	0,02	0,025	0,05
a2	0,01	0,001	0,065	0,025	0,01	0,05	0,01	0,05	0,08

 

13. Если c²_набл < c²_кр, то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо. Если c²_набл > c²_кр – гипотезу отвергают.

 

Задание 2